На координатную ось
Если движение точки задано естественным способом, то ее ускорение определяют с помощью теоремы о проекции ускорения на касатель-
ную и нормаль; если движение точки задано координатным способом — то с помощью теоремы о проекции ускорения на координатную ось.
Теорема.Проекция ускорения на координатную ось равна второй производной от соответствующей координаты по времени.
Из доказанной в предыдущем параграфе теоремы видно, что проекция скорости точки на координатную ось равна скорости проекции точки на ту же ось.
Аналогичное положение будет справедливо и для ускорения точки, т. е. проекция ускорения точки на координатную ось равна ускорению проекции точки на ту же ось. Так как проекции точек на оси движутся прямолинейно, то, согласно § 9.5,
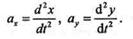
|
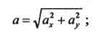
|
Зная две проекции ускорения, можно найти модуль и направление полного ускорения по формулам: модуль ускорения
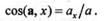
|
направление ускорения
Пример 9.9. Движение точки определяется уравнениями
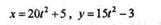
(t — в секундах, х и у — в метрах). Определить модуль и направление скорости и ускорения в момент времени t = 2 с.
Решение. Для определения модуля и направления скорости точки применим теорему о проекции скорости на координатную ось. Продифференцировав по времени уравнения движения точки, получим:
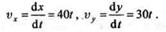
|
Модуль скорости точки определим по формуле
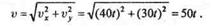
Подставив значение времени t = 2с, получим
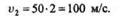
Направляющий косинус определим по формуле
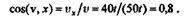
Для определения модуля и направления ускорения точки применим теорему о проекции ускорения на координатную ось. Второй раз продифференцировав по времени уравнения движения точки, получим:
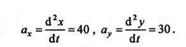
|
Модуль ускорения точки определяем по формуле
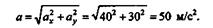
|
Направляющий косинус определится по формуле
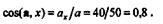
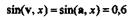
|
| Угол между векторами v, а и осью х будет углом первой четверти, так как |
есть величина положительная.
Так как направление вектора скорости в любой момент времени остается неизменным, то движение точки является прямолинейным и полное ее ускорение можно определить по формуле
Глава 10
Дата добавления: 2021-09-07; просмотров: 612;











