Поступательное движение

Различают два вида простейших движений твердого тела: поступа­тельное движение и вращение вокруг неподвижной оси.

Движение тела, при котором любая прямая, проведенная в теле, ос­тается параллельной своему первоначальному положению, называется поступательным. Представление о поступательном движении мож­но получить, наблюдая движение кузова вагона трамвая на прямолиней­ном участке пути, поступательно движется стол продольно-строгального станка, поршень стационарного двигателя внутреннего сгорания и т. п.

Теорема.При поступательном движении все точки твердого тела имеют одинаковые траектории, скорости и ускорения.

Пусть за время t тело, двигаясь поступательно, переместилось из положения АВ в положение А₁В₁,причем произвольная точка А прошла путь s_A, а другая произвольная точка В прошла путь s_B (рис. 10.1):

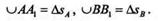
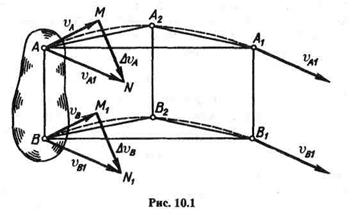
Соединим точки А и А₁, В и В₁хордами. Так как АВ = А₁В₁(тело твердое) и АВ || А₁В₁(движение поступательное), то фигура АВВ₁А₁

есть параллелограмм. Следовательно, хорда АА₁равна и параллельна хорде ВВ₁.

Возьмем промежуточное положение прямой А₂В₂и соединим концы этого отрезка с точками А и А₁, В и В₁,как показано на рисунке.

Аналогично предыдущему можно доказать, что вписанные ломаные линии АА₂А₁и ВВ₂В₁ имеют попарно равные и параллельные стороны. Если бесконечное число раз удваивать число сторон этих ломаных линий, то в пределе они дадут дуги s_A и s_B. Но так как эти ломаные линии все­гда одинаковы, то они одинаковы и в пределе, следовательно, траектории произвольных точек А и В будут одинаковы:

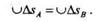
Так как точки А и В выбраны совершенно произвольно, то, следова­тельно, траектории всех точек тела будут одинаковы.

Докажем теперь, что скорости и ускорения точек А и В,а следова­тельно, и всех точек тела в каждый данный момент времени равны. Так как векторы перемещений точек А и В равны между собой:

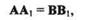
то, разделив обе части этого векторного равенства на t и перейдя к пре­делу при t, стремящемся к нулю, получим

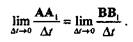
Согласно § 9.4, эти пределы дают векторы скоростей точек, следова­тельно,

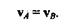
Перенесем векторы скоростей v_A1 и v_B1 в точки А и В инайдем векто­ры приращения скоростей v_A и v_B. Рассмотрим треугольники AMN и BM₁N₁.Эти треугольники конгруэнтны (равны), и их равные стороны по­парно параллельны, следовательно,

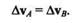
Разделим обе части этого векторного равенства на t и перейдем к пределу при t, стремящемся к нулю, в результате чего получим

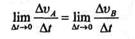
или

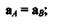
теорема доказана.

Таким образом, поступательное движение твердого тела вполне оп­ределяется движением одной из его точек, следовательно, все формулы кинематики точки применимы для тела, движущегося поступательно.

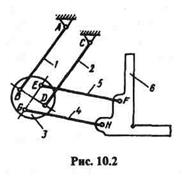
Пример 10.1. Звенья 1 и 2 механизма чертежного приспособления (рис. 10.2) мо­гут поворачиваться относительно опор А и С и шарнирно соединены с диском 3,диск и линейка 6 шарнирно соединены звеньями 4 и 5.Доказать, что диск 3 и линейка 6 будут совершать поступательное движение, если АВ = CD, AC = BD, EF = GH, EG = FH.

Решение. Рассмотрим четырехугольник ABDC. Так как противоположные стороны этого четырехугольника по условию попарно равны, то он представляет собой параллело­грамм. Отсюда следует, что при любом пе­ремещении звеньев 1 и 2 сторона BD остает­ся параллельной неподвижной стороне АС.Таким образом, согласно определе­нию поступательного движения, сторона BD и жестко связанный с нею диск мо­гут перемещаться только поступательно. Так же только поступательно может перемещаться и отрезок EG, жестко связанный с диском 3.

Далее рассмотрим четырехугольник EFHG,который по условию является параллелограммом при любом положении механизма. Следовательно, сторона FH движется так же, как сторона EG, т. е. поступательно. Очевидно, что линейка 6, жестко связанная со стороной FH,также может двигаться только поступательно.

В приведенном примере предполагалось, что звенья механизма представля­ют собой абсолютно твердые тела.