Ускорение точки в криволинейном движении

При движении точки по криволинейной траектории скорость меняет свое направление.

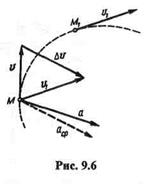
Представим себе точку М,которая за время t, двигаясь по криволи­нейной траектории, переместилась в положение М₁(рис. 9.6).

Вектор приращения (изменения) скоро­сти обозначим v, тогда

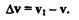
Дня нахождения вектора v перенесем век­тор v₁ в точку М и построим треугольник скоро­стей. Определим вектор среднего ускорения:

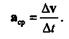
Вектор а_ср параллелен вектору v, так как от деления векторной величины на ска­лярную направление вектора не меняется. Вектор истинного ускорения есть предел, к которому стремится отношение вектора приращения ско­рости к соответствующему промежутку времени, когда последний стремится к нулю:

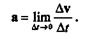
Такой предел называют векторной производной. Таким образом, истинное ускорение точки в криволинейном движении равно векторной производной скорости по времени.

Из рис. 9.6 видно, что вектор ускорения в криволинейном движении всегда направлен в сторону вогнутости траектории.

Так как векторную производную непосредственно вычислять мы не умеем, то ускорение в криволинейном движении будем определять кос­венными путями. Так, например, если движение точки задано естествен­ным способом, то применяется теорема о проекции ускорения на каса­тельную и нормаль. К изучению этой теоремы перейдем, предварительно рассмотрев вопрос о кривизне кривых линий.