Ускорение точки в прямолинейном движении
Ускорение есть кинематическая мера изменения вектора скорости точки.
Ускорение есть величина векторная. При прямолинейном движении точки вектор скорости всегда совпадает с траекторией и поэтому вектор изменения скорости также совпадает с траекторией.
Из курса физики известно, что ускорение представляет собой изменение скорости в единицу времени. Если за небольшой промежуток времени  t скорость точки изменилась на
t скорость точки изменилась на 
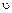 , то среднее ускорение
, то среднее ускорение
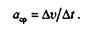
Среднее ускорение не дает представления об истинном ускорении в каждый данный момент времени (истинное ускорение иначе называют мгновенным). Чем меньше промежуток времени, за который определяют среднее ускорение, тем ближе оно к истинному. Истинное ускорение есть предел, к которому стремится среднее ускорение при  t, стремящемся к нулю:
t, стремящемся к нулю:
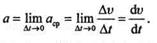
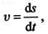
|
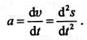
|
| получаем |
| Таким образом, учитывая, что |
Истинное ускорение в прямолинейном движении равно первой производной скорости или второй производной координаты (расстояния от начала отсчета перемещения) по времени.
Единица ускорения
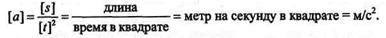
|
Пример 9.4. Точка движется прямолинейно по закону s = t4 +2t (s — в метрах, t — в секундах). Найти ее среднее ускорение в промежутке между моментами t1 =5 с, t 2 = 7 с, а также ее истинное ускорение в момент t 3 = 6 с.
Решение. Сначала определяем скорость точки:
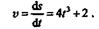
|
Подставляя сюда вместо t его значения t 1= 5 с и t2= 7 с, находим:
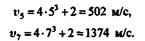
|
Следовательно, приращение скорости за данный промежуток времени
 t = 7 - 5 = 2 с будет
t = 7 - 5 = 2 с будет
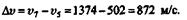
Среднее ускорение точки
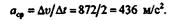
|
Чтобы определить истинное ускорение точки, находим производную от скорости по времени:
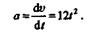
Подставляя сюда вместо t значение t 3 = 6 с, получаем
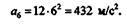
Дата добавления: 2021-09-07; просмотров: 463;











