Способы задания движения точки

Знание законов движения тела означает знание законов движения каждой его точки, поэтому изучение кинематики начнем с изучения дви­жения геометрической точки.

Траекторией точки называется множество (геометрическое место) положений движущейся точки в рассматриваемой системе отсчета.

В зависимости от формы траектории движение точки бывает двух видов: прямолинейное и криволинейное. Рассмотрим два способа задания движения точки естественный и координатный.

Естественный способ заключается в том, что движение точки задается ее траекторией, началом отсчета и уравнением движения по этой траектории (законом движения)

Уравнение движения в общем виде записывается следующим образом:

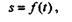
где s — расстояние точки от начального положения, являющееся функци­ей времени; t — время движения точки от начального момента

Зная траекторию точки и уравнение движения по этой траектории, можно определить положение точки в любой момент времени, для чего следует в равенство s = f(t) подставить время.

При своем движении точка проходит некоторый путь, также являю­щийся функцией времени. Следует подчеркнуть, что путь, пройденный точкой, совпадает с расстоянием от начала отсчета лишь тогда, когда точка все время движется в одном направлении и начало ее движения совпадает с началом отсчета.

Координатный способ заключается в том, что движение точки задается движением ее проекций вдоль осей координат.

Уравнения плоского движения точки в координатной форме записы­ваются следующим образом:

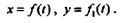
Зная уравнения движения точки в координатной форме, можно, под­ставив в эти уравнения время, определить положение проекций точки, а следовательно, и самой точки в любой момент времени (рис 9.2).

Для того чтобы при координатном способе задания движения точки определить уравнение траектории у = f(x), необходимо из уравнений движения исключить время.

Международная система единиц (СИ) устанавливает в качестве еди­ницы длины м е т р, а в качестве единицы времени — секунду.

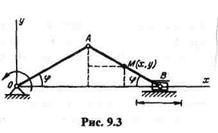
Пример 9.1. Кривошип ОА вращается около неподвижной оси так, что угол 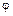= 10t рад. Длина ОА = АВ = 0,8 м. Найти уравнения движения и траекторию средней точки М шатуна, а также уравнение движения ползуна В,если в началь­ный момент ползун находится в крайнем положении; оси координат указаны на рис. 9.3.

Решение. Определим координаты точки М в зависимости от угла :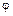

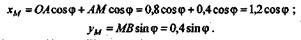
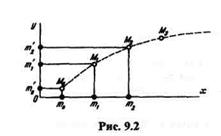
Таким образом, уравнения движения точки М запишутся так

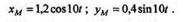
Чтобы определить уравнение траектории точки М, исключим из уравнений движения время. Преобразуем уравнения движения и возведем их в квадрат:

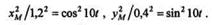
Сложив правые и левые части этих равенств, получим уравнение траектории точки М:

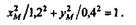
Точка М движется по эллипсу с полуосями длиной 1,2 и 0,4 м. Так как пол­зун В движется прямолинейно вдоль оси х, то у_B = 0.

Для получения уравнения движения ползуна определим абсциссу точки В в зависимости от угла :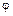

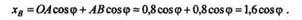
Тогда уравнение движения ползуна запишется так:

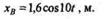
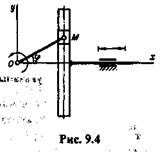
Пример 9.2. Кривошип ОМ кулисы Вольфа равномерно вращается около неподвижной оси О так, что угол 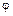= ( 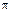/4)t, рад (рис 9.4). Длина стержня ОМ= 0,2 м.

В начальный момент стержень ОМ составил с осью Ох угол 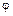₀ = 0. Составить уравнение дви­жения кулисы.

Решение. Из конструкции механизма вид­но, что кулиса движется возвратно-поступа­тельно вдоль оси х. Очевидно, что кулиса будет двигаться по тому же закону, по которому дви­жется проекция точки М на ось x, следователь­но,

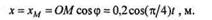
Скорость точки

Скорость есть кине­матическая мера движения точки, характеризующая бы­строту изменения ее положе­ния.

Как известно из физики, при равномерном движении скорость измеряется длиной пути, пройденного за единицу времени:

v = s/t = const

(предполагается, что начала отсчета пути и времени совпадают). Единица скорости

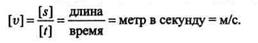
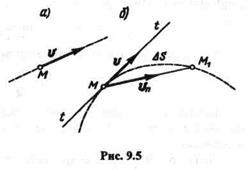
Скорость есть величина векторная. При прямолинейном равномер­ном движении скорость постоянна и по модулю, и по направлению, а век­тор ее совпадает с траекторией (рис. 9.5, а).

При криволинейном движении скорость точки по направлению ме­няется. Для того чтобы установить направление вектора скорости при криволинейном движении, разобьем траекторию на бесконечно малые участки пути, которые можно считать вследствие их малости прямоли­нейными. Тогда на каждом участке условная скорость 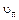такого прямоли­нейного движения будет направлена по хорде. В пределе при s,стремя­щемся к нулю, хорда совпадает с касательной, следовательно, скорость в каждый момент времени направлена по касательной к траектории в сторону движения (рис. 9.5, б).

При неравномерном движении точки модуль ее скорости меняется. Представим себе точку, движение которой задано естественным спосо­бом уравнением

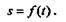
Если за небольшой промежуток времени t точка прошла путь s,то ее средняя скорость равна

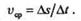
Средняя скорость не дает представления об истинной скорости в ка­ждый данный момент времени (истинную скорость иначе называют мгновенной). Чем меньше промежуток времени, за который определяется средняя скорость, тем ближе она к истинной.

Истинная скорость есть предел, к которому стремится средняя ско­рость при t,стремящемся к нулю:

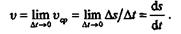
Таким образом, числовое значение скорости равно

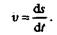
Истинная скорость при любом движении точки равна первой про­изводной координаты (т. е. расстояния от начала отсчета перемещения) по времени.

Движение, в котором скорость с течением времени возрастает, назы­вают ускоренным; движение, в котором скорость с течением време­ни уменьшается, — замедленным.

Пример 9.3. Поезд движется согласно уравнению

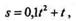
где t — в секундах, s — в метрах.

Определить среднюю скорость поезда за промежуток времени между кон­цом 10-й и 20-й секунд и истинную скорость в конце 20-й секунды.

Решение. Для определения средней скорости поезда найдем приращения времени и пути за указанный промежуток времени:

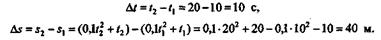
Средняя скорость поезда определится так:

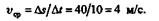
Для определения истинной скорости поезда продифференцируем уравнение движения по времени, в результате чего получим формулу, выражающую зависи­мость истинной скорости от времени:

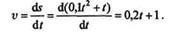
Подставив в это выражение время t₂,получим значение истинной скорости в конце 20-й секунды:

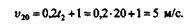
Пусть точка из положения М,двигаясь неравномерно, за время t перешла в положение М₁(рис. 9.5, б). Дугу ММ₁обозначим s. Отрезок ММ₁ назовем вектором перемещения точки М.Допустим, что точка М перешла за время t в положение М₁, двигаясь по хорде и притом равно­мерно, тогда скорость такого прямолинейного движения будет

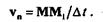
Перейдем к пределу, умножив предварительно числитель и знамена­тель правой части на s, и представим предел произведения как произве­дение пределов:

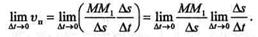
Так как при t, стремящемся к нулю, s также стремится к нулю, то первый предел (предел отношения хорды к соответствующей дуге) равен единице. Второй предел дает первую производную пути по времени, т. е. истинную скорость, причем вектор v_п в пределе будет направлен по каса­тельной, т. е. совпадет с вектором истинной скорости v. Таким образом,

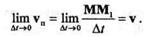
Следовательно, предел вектора условной скорости v_п, равный преде­лу отношения вектора перемещения точки к соответствующему про­межутку времени, когда последний стремится к нулю, равен вектору истинной скорости точки.

В дальнейшем этим выводом пользуются в готовом виде, что позво­ляет упростить математическую часть доказательств некоторых теорем.