Антипараллельных сил
Рассмотрим случай сложения двух не равных по модулю антипараллельных сил. Случай, когда такие силы равны по модулю, особый и рассмотрен в гл. 4.
Теорема.Две неравные антипараллельные силы эквивалентны равнодействующей, которая равна разности данных сил, параллельна им и направлена в сторону большей силы; линия действия равнодействующей делит отрезок, соединяющий точки приложения данных сил, внешним образом на части, обратно пропорциональные этим силам.
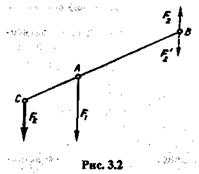
Рассмотрим две параллельные силы F1 и F2, причем F1 > F2 (рис. 3.2). Разложим силу F1 на две параллельные составляющиеF  иF'2 так, чтобы
иF'2 так, чтобы
|
составляющая F'2 была приложена в точке В и F'2 = F2. Тогда на основании
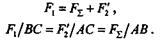
|
Из этих равенств найдем модуль второй составляющей F 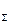 и расстояние и расстояние
|
теоремы о сложении двух параллельных сил, направленных в одну сторону, получим
АС до точки ее приложения (известно, что F'2 = F2).
Данная система сил (F1 ,F2) заменена системой трех сил:
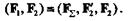
|
Отбросив на основании аксиомы IV две взаимно уравновешенные силы F2 и F'2, получим, что данная система эквивалентна одной силе, т. е.
равнодействующей F 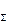 :
:
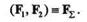
Модуль и точка приложения равнодействующей определяются по формулам
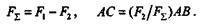
Отметим, что равнодействующая двух параллельных сил равна их алгебраической сумме.
Если на тело действует система л параллельных сил, то, производя последовательное сложение сначала двух сил, их равнодействующей с третьей силой, новой равнодействующей с четвертой силой и т. д., найдем модуль и линию действия равнодействующей всей системы параллельных сил.
Очевидно, что равнодействующая системы параллельных сил определится в результате алгебраического сложения сил данной системы:
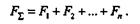
Таким образом, равнодействующая системы параллельных сил равна их алгебраической сумме:
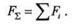
|
Вопрос о положении линии действия равнодействующей легко решается с помощью теоремы, доказанной в § 5.3.
Дата добавления: 2021-09-07; просмотров: 674;











