Основные свойства пары

Основные свойства пары характеризуются следующими тремя тео­ремами.

Теорема I. Пара сил не имеет равнодействующей.

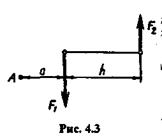
Дана пара (F₁, F₂) с плечом h (рис. 4.2).

Предположим, что F₂> F₁.Тогда равнодействующая этих сил F 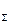= F₂ - F_l , а точка ее приложения определяется из пропорции

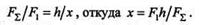
Пусть теперь сила F₂уменьшается и приближается по модулю к силе F₁,тогда в пределе при F₁= F₂

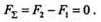
Это значит, что приF₁= F₂ равнодействующая не существует.

Из этой теоремыследует, чтопара сил не может быть уравновеше­на одной силой, пара сил может быть уравновешена только парой.

Теорема П.Алгебраическая сумма моментов сил, составляющих пару, относительно любой точки плоскости действия пары есть вели­чина постоянная, равная моменту пары.

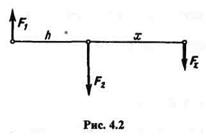
Дана пара (F₁, F₂) с плечом h (рис. 4.3) и моментом т = F₁h= F₂h.

Выберем в плоскости действия пары произвольную точку А и при­мем ее за центр моментов:

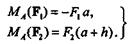
Сложим правые и левые части этих равенств: M_A (F₁) + M_A(F₂)= -F₁a + F₂(a + h)= F₂h,или

M_A (F₁) + M_A(F₂)= m;теорема доказана.

Из этой теоремы следует, что при любом центре моментов пара сил войдет в уравнение моментов с одним и тем же знаком и одной и той же величиной.

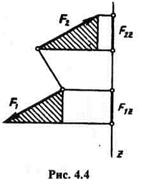
Теорема Ш.Алгебраическая сумма про­екций сил пары на ось всегда равна нулю.

Дана пара (F₁, F₂) и ось z,лежащая в плос­кости действия пары (рис. 4.4). Из равенства заштрихованных треугольников видно, что F_1z = F_2z. Проекция F_1z — положительная, про-

екция F_2z— отрицательная, следовательно, их алгебраическая сумма все­
гда равна нулю.

Из этой теоремы следует, что пара сил не входит ни в уравнение сил, ни в уравнение проекций сил.

Эквивалентные пары

Две пары называются эквивалентными, если одну из них мож­но заменить другой, не нарушая механического состояния свободного твердого тела.

Теорема об эквивалентных парахформулируется так: если момен­ты двух пар алгебраически равны, то эти пары эквивалентны.

Даны две пары (F, F₁) и (Q, Q₁), моменты которых алгебраически равны (рис. 4.5), т. е.

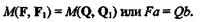
Продолжим линии действия сил пары до их взаимного пересечения в точках А и В.На основании следствия из аксиом III и IV перенесем силы F и F₁ вдоль линий их действия в точки А и В.Соединим эти точки пря­мой линией и разложим силы Fи F₁ по направлению АВ и вдоль линий действия сил Q и Q₁. Из равенства треугольников Akd и Втп вытекает, что Т=Т₁и S = S₁.

Силы Т и T₁ представляют собой уравновешенную систему, так как они равны по модулю и действуют по одной прямой в противоположные стороны. На основании аксиомы IV такую систему можно отбросить.

Силы S и S₁ представляют собой пару сил с плечом b.Таким обра­зом, пара (F, F₁) 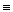паре (S, S₁).

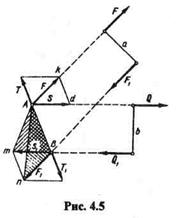
Рассмотрим треугольники АтВ и АпВ.Они имеют общее основание

АВ, а высоты их равны, следовательно,

пл. АтВ - пл. АпВ.

Но удвоенная площадь 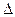АпВ чис­ленно равна моменту пары (F, F₁), а уд­военная площадь 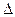АтВ численно равна моменту пары (S, S₁), следовательно, М(F,F₁) = M(S, S₁) или Fa = Sb.

По условиям теоремы Fa = Qb,следо­вательно, Sb = Qb,отсюда S= Q, S₁ = Q₁.

Силы S и Qравны по модулю, дейст­вуют по одной прямой в одну сторону, следовательно, они эквивалентны друг другу; на этом же основании эквивалентны

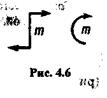
друг другу силы S₁ и Q₁. Следовательно, пара (Q, Q₁) 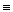паре (S, S₁).

Но выше доказано, что пара (F, F₁) 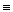паре (S, S₁).

Так как две пары порознь эквивалентны одной и той же третьей паре, то эти пары эквивалентны между собой, т. е.

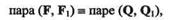
что и требовалось доказать.

Из доказанной теоремы об эквивалентных парах вытекает четыре следствия:

1) не изменяя механического состояния тела, пару можно переме­щать как угодно в плоскости ее действия;

2) не изменяя механического состояния тела, можно менять силы и плечо пары, но так, чтобы ее момент оставался неизменным;

3) чтобы задать пару, достаточно задать ее момент, поэтому иногда слово «пара» заменяют словом «момент» и условно изображают его так, как показано на рис. 4.6;

4) условия равновесия плоской системы параллельных сил будут справедливы, если вместе с такой системой действуют и пары сил, так как их можно повернуть в плоскости действия и поставить силы пары парал­лельно другим силам системы.