Если импульс сохраняется в одной инерциальной системе, то он сохраняется и в любой другой системе, движущейся относительно нее с произвольной скоростью прямолинейно и равномерно.

Лекция 6

Сила. Уравнение движения Ньютона. Работа. Кинетическая энергия. Консервативные и неконсервативные силы.

Итак, для того чтобы определить движение материальной точки, надо решить уравнение движения Ньютона

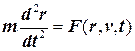, (6.1)

где сила F в общем случае может зависеть от:

- координат частицы r(колебания груза па пружине, F=-kx, движение Земли вокруг Солнца, F~1/r²);

- скорости частицы v (сила трения: при больших скоростях ~ υ²,
а при малых ~ υ)

- времени t (переменное во времени воздействие).

Однако, как известно, заданием силы движение однозначно еще не определяется. Необходимо задать также начальные условия r(0)и υ(0),то есть значения координаты и скорости в некоторый начальный момент времени t. Тогда, как доказывается в математике, уравнение (6.1) будет иметь единственное решение r= r(t).

Поскольку в уравнение, описывающее второй закон Ньютона, входят не только сама функция r(t), но и ее первая, dr/dt= υ, и вторая, d²r/dt² = а, производные по времени, это уравнение называется дифференциальным уравнением второго порядка.

Работа

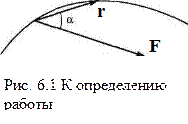Как известно из курса физики средней школы, работа — это скалярная величина, равная произведению силы на перемещение и на косинус угла между ними. Для конечного перемещения ∆r имеем:

∆A = F ∆r = F ∆r соs α,

где мы воспользовались понятием скалярного произведения двух векторов.

В общем случае, когда материальная точка, двигаясь по криволинейной траектории L, проходит путь конечной длины, этот путь можно мысленно разбить па бесконечно малые участки, на каждом из которых сила F может считаться приближенно постоянной, а элементарная работа может быть вычислена по формуле dA = F • dr. Если теперь сложить все эти элементарные работы, то получим выражение для работы в виде интеграла

А = ò F dr. (6.2)

Это выражение называется криволинейным интеграломот вектора F вдоль кривой L. Работа силы, отнесенная к единице времени, называется мощностью:

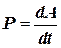(6.3)

Поскольку dA = F • dr, то формулу для работы можно переписать в виде

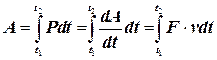(6.4)

то есть можно выразить работу через интеграл от мощности по времени, или через интеграл по времени от скалярного произведения силы на скорость частицы. В последнем случае ясно, что если сила, действующая на частицу, перпендикулярна скорости v, то работа такой силы равна нулю.

Воспользуемся теперь формулой второго закона Ньютона и выразим силу через производную от импульса по времени F = dp/dt:

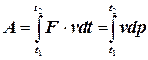(6.5)

Поскольку р=mv, то dp = mdv. Поэтому

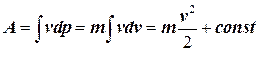. (6.6)

Если теперь мы будем рассматривать работу силы при перемещении материальной точки из положения 1 в положение 2, то искомая работа будет равна

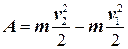(6.7)

Как известно, скалярная величина

K= 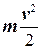(6.8)

называется кинетической энергией частицы. Таким образом, мы доказали, что работа силы по перемещению материальной точки равна приращению ее кинетической энергии.

При этом под силой надо, однако, понимать полную силу, действующую на точку. Так, например, если вы тащите санки по не очень скользкой дороге (посыпанной песком), то работа, которую вы совершаете, отлична от нуля. Однако никакого приращения кинетической энергии санок не происходит. Все дело в том, что сила трения тоже производит работу (отрицательную). В результате полная сила и полная работа оказываются равными нулю.

Полученный результат может быть без труда обобщен на случай произвольной системы материальных точек. Кинетической энергией системы называется сумма кинетических энергий материальных точек, из которых состоит эта система:

К = å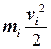

В результате: