Основные законы физики одинаково формулируются для всех систем отсчета, которые движутся относительно друг друга с постоянной скоростью (то есть без ускорения).
Согласно этому принципу, наблюдатель, находящийся в кабине без окон, не может экспериментально определить, покоится он или находится в равномерном прямолинейном движении. Только глядя в окно и имея, таким образом, возможность сравнивать свое движение с движением окружающих тел, наблюдатель может сказать, что он равномерно движется относительно них. Но даже и тогда он не мог бы решить, сам ли он движется или движутся тела.
Принцип относительности Галилея был одним из первых основных принципов физики. Он является основным для картины Вселенной, предложенной Ньютоном. Этот принцип выдержал многократную экспериментальную проверку.
Постараемся теперь придать принципу относительности Галилея математическую форму. Обозначим через Sкакую-либо инерциальную декартову систему координат, а через S' — другую инерциальную декартову систему координат, которая движется со скоростью V относительно первой. Пусть x', у', z', оси системы S’, направлены параллельно осям х, у, z системы S. Выберем эти оси так, чтобы вектор V был направлен параллельно оси х. Мы хотим сравнить результаты измерения времени и расстояний, которые сделаны неподвижным относительно системы S наблюдателем, с такими же измерениями, которые выполнены наблюдателем, покоящимся относительно системы S’. Каким будет результат такого сравнения, можно будет окончательно решить только с помощью опыта.
Экспериментально мы находим, что
L' = L (V«c). (4.4)
Мы можем теперь выразить равенства t' = t и L’=L в виде преобразования, связывающего координаты х', у', z' и время t' какого-либо события, измеренные в системе S’, с координатами x, у, z, и временем t этого же события в системе S. Предположим, что в начальный момент времени, который одинаков для обеих систем, то есть при t=0 и t’=0, начала координат обеих систем совпадают. Тогда, если мы выберем совершенно одинаковые масштабы длин, то получим следующие уравнения преобразования:
t =t’, х=x’+ υt, y = y', z=z’. (4.5)
Это преобразование называется преобразованием Галилея.В векторной форме его, очевидно, можно записать так:
r=r' + υt', t=t'. (4.6)
Если сопоставить преобразование Галилея с основным постулатом о том, что законы физики, определенные в системах S и S’, должны быть тождественными, то мы можем сделать такой вывод.
Основные законы физики должны быть инвариантными относительно преобразований Галилея.
Этот вывод имеет более частныйхарактер, чем принцип относительности Галилея, так как мы считали, что скорость света бесконечна, из чего следовало, что можно одновременно синхронизировать часы в обеих системах отсчета, то есть что t' = t. На самом деле из-за конечности скорости света основными преобразованиями, относительно которых должны быть инвариантными все законы природы, являются преобразования Лоренца,а не Галилея.
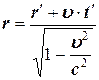
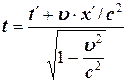 (4.7)
(4.7)
Именно они адекватно выражают принцип относительности Галилея (не путать: принцип относительности Галилея верен точно, а преобразования Галилея — приближенно при условии, что υ<< с).
Рассмотрим законы Ньютона применительно для вращательного движения. Во-первых, введем понятие аналогичное материальной точке.
Абсолютно твердое тело – тело, расстояние, между точками которого не меняется при движении этого тела.
Если воздействовать на тело равными силами 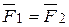 , но приложенными в разные точки (на расстоянии r1 и r2 от оси вращения,
, но приложенными в разные точки (на расстоянии r1 и r2 от оси вращения, 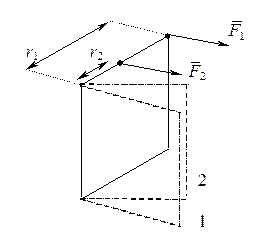 соответственно), то, если сила является мерой воздействия в случае вращательного движения, результат воздействия должен быть одинаковым. Однако из эксперимента видно, что он разный. В первом случае угловое ускорение будет больше, чем во втором и, соответственно, угловой путь, пройденный телом за одинаковое время в первом случае больше, чем во втором (φ1 >φ2).
соответственно), то, если сила является мерой воздействия в случае вращательного движения, результат воздействия должен быть одинаковым. Однако из эксперимента видно, что он разный. В первом случае угловое ускорение будет больше, чем во втором и, соответственно, угловой путь, пройденный телом за одинаковое время в первом случае больше, чем во втором (φ1 >φ2).
Следовательно, сила не является мерой воздействия при вращательном движении. В качестве меры воздействия вводится понятие момента силы.
 Момент силы равен векторному произведению радиус вектора
Момент силы равен векторному произведению радиус вектора 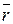 , проведенному от оси вращения в точку приложения силы
, проведенному от оси вращения в точку приложения силы 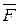 , на эту силу, т.е.
, на эту силу, т.е.
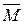 = [
= [ 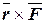 ]. (4.8)
]. (4.8)
Величина момента силы
М = F r sina,
где a – угол между векторами 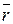 и
и 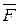 .
.
Направление вектора момента силы 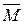 может быть определено по "правилу правого винта”: если при вращении правого винта вектор силы касателен к этому вращению, то поступательное движение винта совпадает по направлению с вектором момента силы
может быть определено по "правилу правого винта”: если при вращении правого винта вектор силы касателен к этому вращению, то поступательное движение винта совпадает по направлению с вектором момента силы 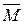 , т.е. M ^ F и r.
, т.е. M ^ F и r.
Рассмотрим движение по наклонной плоскости двух цилиндров одинаковой массы (m1=m2), одинаковых геометрических размеров ( d1 = d2,  l1=l2), с одинаковым материалом поверхности (коэффициенты трения одинаковы, k1= k2), т.е. силы, действующие на цилиндры одинаковы, но имеющих разное распределение масс по объему (первый – сплошной, второй – полый). Если масса является мерой инертности тела, то к основанию наклонной плоскости оба цилиндра должны скатиться одновременно. Однако из эксперимента видно, что первый цилиндр скатывается быстрее, чем второй.
l1=l2), с одинаковым материалом поверхности (коэффициенты трения одинаковы, k1= k2), т.е. силы, действующие на цилиндры одинаковы, но имеющих разное распределение масс по объему (первый – сплошной, второй – полый). Если масса является мерой инертности тела, то к основанию наклонной плоскости оба цилиндра должны скатиться одновременно. Однако из эксперимента видно, что первый цилиндр скатывается быстрее, чем второй.
Масса не является мерой инертности при вращательном движении а.т.т.
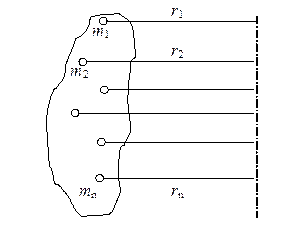 В качестве меры инертности вводится понятие момента инерции.
В качестве меры инертности вводится понятие момента инерции.
Момент инерции тела относительно неподвижной оси равен сумме произведений масс всех материальных точек тела на квадраты их расстояний до оси:
I = 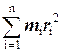 (4.9)
(4.9)
Таким образом, основываясь на законах Ньютона, можно записать законы динамики вращательного движения твердого тела.
Основной закон динамики вращательного движения твердого тела. Если моменты сил, действующие на тело, не скомпенсированы, то тело будет двигаться с угловым ускорением, величина которого пропорциональна результирующему моменту сил и обратно пропорционально моменту инерции.
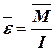 (4.10)
(4.10)
Подсчитаем моменты инерции некоторых тел
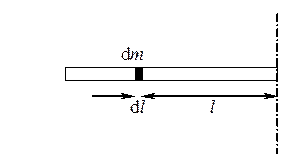 а) момент инерции стержня относительно оси, проходящей через конец стержня перпендикулярно к нему.
а) момент инерции стержня относительно оси, проходящей через конец стержня перпендикулярно к нему.
На стержне выделим элементарный отрезок размером dl на расстоянии l от оси вращения. Элементарная масса dm отрезка стержня размером dl может быть найдена как
dm = t dl,
где t = 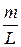 – линейная плотность стержня.
– линейная плотность стержня.
Момент инерции отрезка dl массой dm, находящегося на расстоянии l от оси вращения
dI = 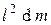 .
.
Тогда момент инерции всего стержня
I = 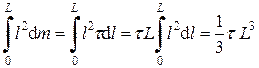 .
.
Так как масса стержня m = t L, то
I = 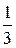 mL2
mL2
б) момент инерции диска относительно оси, проходящей через центр диска перпендикулярно к нему.
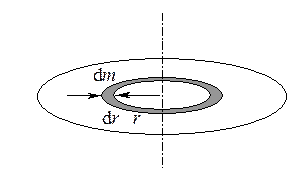
На диске выделим кольцо толщиной dr на расстоянии r от оси вращения. Элементарная масса dm кольца толщиной dr может быть найдена как
dm =s ds = s 2pr dr,
где s = 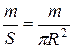 – поверхностная плотность диска.
– поверхностная плотность диска.
 Момент инерции кольца толщиной dr массой dm, находящегося на расстоянии r от оси вращения
Момент инерции кольца толщиной dr массой dm, находящегося на расстоянии r от оси вращения
dI = 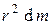 .
.
Тогда момент инерции всего диска
I = 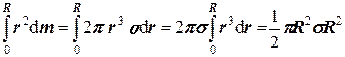 .
.
Так как масса диска m = pR2s , то
I = 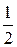 m R2.
m R2.
в) момент инерции сплошного однородного шара относительно оси, проходящей через его центр.
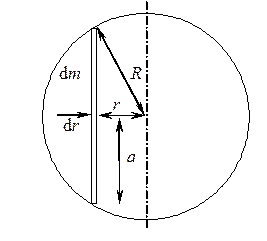 В шаре вырежем кольцо толщиной dr на расстоянии r от оси вращения. Момент инерции кольца радиусом а =
В шаре вырежем кольцо толщиной dr на расстоянии r от оси вращения. Момент инерции кольца радиусом а = 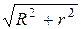 и массой dm равен
и массой dm равен
dI = 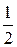
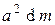 .
.
Масса кольца
dm = r dV = r pa2 dr = r p (R2– r2) dr,
где r – объемная плотность шара.
Тогда момент инерции
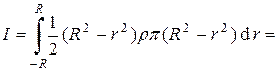
= 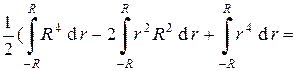 rp(R5 –
rp(R5 – 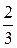 R5 +
R5 + 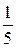 R5) =
R5) = 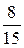 rpR5.
rpR5.
Так как масса шара m = 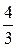 pR3r, то
pR3r, то
I = 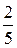 m R2.
m R2.
Теорема Штейнера
Для нахождения момента инерции тел относительно произвольных осей используется теорема Штейнера.
Момент инерции I тела относительно произвольной оси равен сумме момента инерции I0 тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a2 между осями.
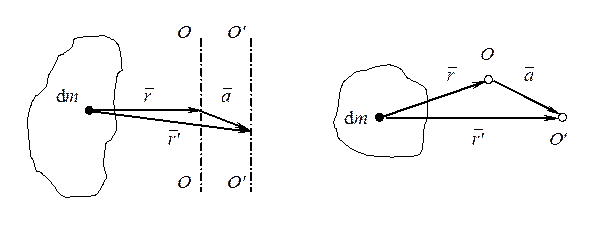 I = I0 + m a2 (4.11)
I = I0 + m a2 (4.11)
Лекция 5
Дата добавления: 2017-09-01; просмотров: 1008;











