Импульс замкнутой системы материальных тел является величиной постоянной, т.е. суммарный импульс системы тел не изменяется.

Подставляя сюда выражение для импульсов частиц, получаем после следующей цепочки преобразований:

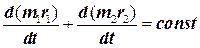. (5.8)

Разделив обе части последнего равенства на суммарную массу, т =m₁ + m₂, получаем уравнение:

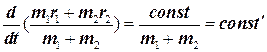. (5.9)

Введем теперь вектор

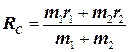. (5.10)

Точка с координатами R_c называется центром инерции(или центром масс)системы из двух материальных точек. Из уравнения (5.9) следует, что, каким бы сложным ни казалось движение каждой из масс, производная dR_c/dt = const. Таким образом, центр инерции движется с постоянной скоростью (независимо от наличия колебательного и вращательного движения системы). Обозначим эту скорость как V_c:

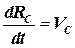(5.11)

Подставляя сюда выражение для R_c и дифференцируя, получаем

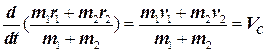(5.12)

Эта формула определяет скорость центра инерции V_C через массы и скорости составляющих систему частиц. К движению именно этой точки относится первый закон Ньютона, и скорость этой точки надо считать скоростью движения системы как целого. Если мы согласимся на такое определение скорости движения системы как целого, то тогда импульс системы как целого должен быть равен произведению суммарной массы системы на ее скорость V_c, то есть (m₁ +m₂)V_c. С другой стороны,

(m₁ + m₂)V_C = m₁ V₁ + m₂v₂ = p₁ + p₂ (5.13)

и импульс системы оказывается равным сумме импульсов составляющих ее частиц. Таким образом, импульс, как говорят, — величина аддитивная,то же самое можно сказать и о массе тела. Мы показали, что в отсутствие внешних сил этот импульс не меняется со временем, то есть сохраняется. Очевидно, что все вышесказанное можно отнести и к системе с большим числом материальных точек. Если на систему теперь действуют внешние силы, например на первое тело F₁ и на второе F₂, то уравнения движения для каждой из материальных точек запишутся в виде:

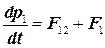
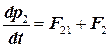
Складывая эти уравнения, получаем

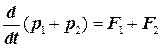, (5.14)

или

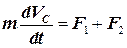. (5.15)

Отсюда следует, что

центр масс системы движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила — геометрической сумме всех внешних сил, действующих на систему.

Примером может служить движение снаряда по параболе в безвоздушном пространстве. Если в какой-либо момент времени снаряд разорвется на мелкие осколки, то эти осколки будут далее разлетаться в разные стороны. Однако центр масс осколков и газов, образовавшихся при взрыве, будет продолжать свое движение по параболической траектории, как если бы никакого взрыва не было.

Сформулировав принцип относительности Галилея и законы Ньютона, мы нашли, что они не противоречат друг другу, то есть второй закон Ньютона инвариантен относительно преобразований Галилея. Затем из второго и третьего законов Ньютона мы вывели закон сохранения импульса (этих двух законов, по существу, достаточно: первый закон — частный случай второго, когда сила равна нулю). Таким образом, закон сохранения импульса не противоречит принципу относительности Галилея.