Импульс. Момент импульса. Закон сохранения импульса.
Второй закон Ньютона можно переписать в таком виде:
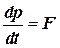 , (5.1)
, (5.1)
где мы ввели величину
р= mv, (5.2)
называемую в физике импульсом.При этом мы предполагали, что масса частицы т от скорости (а значит и от времени) не зависит: ma=  .
.
Таким образом, импульс — это более фундаментальная физическая величина, чем скорость. Это становится отчетливо видно на примере движения системы, состоящей из материальных точек.
Из основного закона движения динамики вращательного движения твердого тела 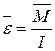 , можно записать с учетом, что
, можно записать с учетом, что  =
= 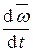 ,
,
тогда
 = I
= I 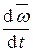 =
=  (5.3)
(5.3)
или
 dt =
dt = 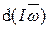 =
= 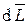 . (5.4)
. (5.4)
Вектор  =
= 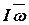 называется моментом импульса. Эта величина, как и импульс тела при поступательном движении, является важной динамической характеристикой.
называется моментом импульса. Эта величина, как и импульс тела при поступательном движении, является важной динамической характеристикой.
Рассмотрим свободное движение двух тел с массами m1 и m2, связанных друг с другом пружинкой, которую для простоты мы будем считать невесомой. На эту систему не действуют внешние силы, поэтому, согласно первому закону Ньютона, система должна либо находиться в покое, либо двигаться с постоянной по величине и направлению скоростью. Но скорость каждого из тел в процессе движения сложным образом меняется по величине и направлению, поскольку система одновременно совершает поступательное, колебательноеи вращательноедвижения. Значит, первый закон Ньютона применим не ко всем точкам системы. А тогда где же находится та точка, которая движется с постоянной скоростью? Она существует (хотя бы одна), иначе первый закон Ньютона не был бы справедливым.
Чтобы ответить на поставленный вопрос, запишем уравнение, выражающее второй закон Ньютона, для каждой из материальных точек 1 и 2:
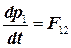
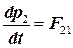
где F12 — сила, действующая со стороны второй частицы на первую, a F21 — сила, действующая со стороны первой частицы на вторую. Согласно третьему закону Ньютона, эти силы равны по величине и противоположны по направлению:
F12=-F21.
Сложим теперь два уравнения движения:
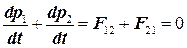 (5.5)
(5.5)
Или
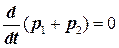 . (5.6)
. (5.6)
В результате получаем закон сохранения импульсасистемы двух тел
P1 + Р2 = const. (5.7)
Дата добавления: 2017-09-01; просмотров: 996;











