Абсолютные и средние показатели вариации и способы их расчета
Для характеристики совокупностей и исчисленных величин важно знать, какая вариация изучаемого признака скрывается за средним.
Для характеристики колеблемости признака используется ряд показателей. Наиболее простой из них – размах вариации.
Размах вариации – это разность между наибольшим ( 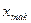 ) и наименьшим (
) и наименьшим ( 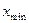 ) значениями вариантов.
) значениями вариантов.
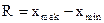
Чтобы дать обобщающую характеристику распределению отклонений, исчисляют среднее линейное отклонение d, которое учитывает различие всех единиц изучаемой совокупности.
Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учета знака этих отклонений:
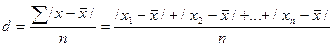 .
.
Порядок расчета среднего линейного отклонения:
1. По значениям признака исчисляется средняя арифметическая:
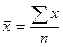 .
.
2. Определяются отклонения каждой варианты 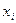 от средней
от средней 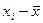 .
.
3. Рассчитывается сумма абсолютных величин отклонений: 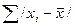 .
.
4. Сумма абсолютных величин отклонений делится на число значений:
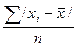 .
.
Если данные наблюдения представлены в виде дискретного ряда распределения с частотами, среднее линейное отклонение исчисляется по формуле средней арифметической взвешенной:
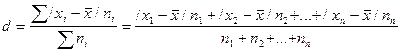
Порядок расчета среднего линейного отклонения взвешенного следующий:
1. Вычисляется средняя арифметическая взвешенная:
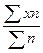 .
.
2. Определяются абсолютные отклонения вариант от средней / 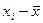 /.
/.
3. Полученные отклонения умножаются на частоты 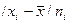 .
.
4. Находится сумма взвешенных отклонений без учета знака:
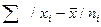 .
.
5. Сумма взвешенных отклонений делится на сумму частот:
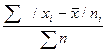 .
.
Дата добавления: 2016-10-18; просмотров: 2879;











