Анализ возмущений сингулярных спектров цифровых изображений при различных возмущающих воздействиях
Погружение секретного сообщения необходимо провести таким образом, чтобы не только обеспечить нечувствительность СС к возмущающим воздействиям, но и надежность его восприятия. Вероятность обеспечения надежности восприятия СС тем больше, чем меньше норма матрицы возмущения контейнера при стеганопреобразовании, при этом, величина нормы матрицы возмущения не зависит от того, какие СНЧ были возмущены, а зависит лишь от абсолютных величин этих возмущений, поэтому для обеспечения надежности восприятия локализация возмущений СНЧ при стеганопреобразовании может рассматриваться как несущественная.
Если  и
и 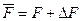 матрицы контейнера и стеганосообщения с СНЧ
матрицы контейнера и стеганосообщения с СНЧ 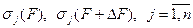 , соответственно, то для них имеет место соотношение (2.6), которое в используемых в данной лекции обозначениях выглядит следующим образом:
, соответственно, то для них имеет место соотношение (2.6), которое в используемых в данной лекции обозначениях выглядит следующим образом:
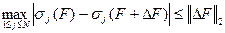 , (8.1)
, (8.1)
где 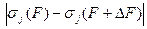 - это возмущение
- это возмущение 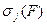 ,
, 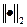 ― спектральная матричная норма, в силу которого возмущения СНЧ сравнимы с возмущением данных ―
― спектральная матричная норма, в силу которого возмущения СНЧ сравнимы с возмущением данных ― 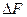 , т.е. СНЧ матрицы являются нечувствительными к возмущающим воздействиям. Однако соотношение (8.1) дает лишь верхнюю границу для возможных возмущений СНЧ, которая может и не достигаться для конкретных СНЧ. Проанализируем детально эти возмущения и определим наименее «уязвимые» при возмущающем воздействии СНЧ, т.е. СНЧ, определяющие
, т.е. СНЧ матрицы являются нечувствительными к возмущающим воздействиям. Однако соотношение (8.1) дает лишь верхнюю границу для возможных возмущений СНЧ, которая может и не достигаться для конкретных СНЧ. Проанализируем детально эти возмущения и определим наименее «уязвимые» при возмущающем воздействии СНЧ, т.е. СНЧ, определяющие 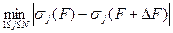 . Будем говорить, что для таких СНЧ степень нечувствительности будет максимальной.
. Будем говорить, что для таких СНЧ степень нечувствительности будет максимальной.
Возмущающее воздействие на контейнер (стеганосообщение) естественно моделировать при помощи наложения на соответствующую матрицу различных шумов. Необходимо отметить, что подходящей и часто используемой моделью для ошибок квантования, возмущающих воздействий при пересылке в канале связи и (или) атак на СС является аддитивный гауссовский шум.
Любое возмущающее воздействие на СС должно сохранить его надежность восприятия, что приводит к необходимости малости нормы матрицы возмущения и, как следствие, к тому, что энергия сигнала-стеганосообщения после возмущающего воздействия должна остаться сравнимой с энергией исходного СС.
Одной из основных характеристик сигнала с матрицей  размера
размера 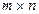 является его энергия
является его энергия 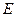 :
:
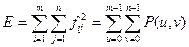 ,
,
где 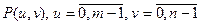 , — энергетический спектр сигнала
, — энергетический спектр сигнала  (лекция 1).
(лекция 1).
Теорема.Энергия двумерного цифрового сигнала  равна сумме квадратов СНЧ его матрицы.
равна сумме квадратов СНЧ его матрицы.
Доказательство. Сингулярное разложение матрицы  представимо в виде суммы внешних произведений:
представимо в виде суммы внешних произведений:
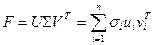 .
.
Такое представление разбивает  на
на 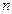 сигналов
сигналов 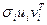 , суммарная энергия которых дает
, суммарная энергия которых дает 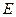 . Энергия сигнала
. Энергия сигнала
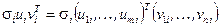
в пространственной области равна:
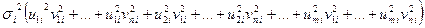
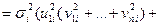
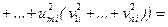
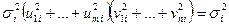 .
.
Таким образом, полная энергия сигнала  определяется как
определяется как 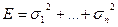 .
.
Следствие. Энергия двумерного цифрового сигнала, матрица которого  является симметричной, равна сумме квадратов СЗ
является симметричной, равна сумме квадратов СЗ  .
.
Очевидно, с большой вероятностью можно предположить что изменения 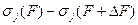 СНЧ при возмущении
СНЧ при возмущении 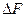 начальной матрицы
начальной матрицы  не могут иметь один знак для всех СНЧ, т.е. среди них будут как положительные, приводящие к тому, что
не могут иметь один знак для всех СНЧ, т.е. среди них будут как положительные, приводящие к тому, что
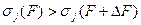 ,
,
так и отрицательные, для которых
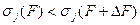 ,
,
 что теоретически должно привести к пересечению графиков сингулярных спектров в подавляющем большинстве случаев, т.е. к наличию СНЧ, возмущения которых в ходе возмущающего воздействия являются нулевыми, а значит эти СНЧ будут нечувствительными к возмущающему воздействию.
что теоретически должно привести к пересечению графиков сингулярных спектров в подавляющем большинстве случаев, т.е. к наличию СНЧ, возмущения которых в ходе возмущающего воздействия являются нулевыми, а значит эти СНЧ будут нечувствительными к возмущающему воздействию.
Выдвинутая гипотеза подтверждается вычислительным экспериментом, проведенным в среде Matlab более, чем с 200 различными изображениями. Типичная картина результатов первого этапа эксперимента представлена на рис.8.2 для наибольших 50 СНЧ матрицы выделенной на рис.8.1 подобласти изображения размерами 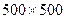 (характер поведения лишь 50 СНЧ представлен для большей наглядности результатов).
(характер поведения лишь 50 СНЧ представлен для большей наглядности результатов).
Второй этап вычислительного эксперимента посвящен анализу характера возмущений СНЧ матриц изображений (типичная картина представлена на рис.8.3 для тестового изображения).
Характер возмущений СНЧ при любом из использованных шумов полностью соответствует выдвинутой гипотезе: наименьшему возмущению (нулевому или сравнимому с нулем) подвергаются СНЧ, находящиеся в окрестности точки пересечения графиков сингулярных спектров исходного и возмущенного изображений (выделенная часть спектра на рис.8.3) (для иллюстрируемого примера – окрестность 15-го СНЧ). Назовем такую зону сингулярного спектра - мертвой зоной (МЗСНЧ). МЗСНЧ, как показывает вычислительный эксперимент, присутствует в сингулярном спектре каждого из рассмотренных изображений при использованных моделях возмущающих воздействий. Наименьшие возмущения имеют также минимальные СНЧ, однако их использование для оговоренных выше целей затруднительно в силу следующей причины: наименьшие СНЧ для подавляющего большинства изображений как в исходном, так и в возмущенном виде близки к 0, их значения не является информативными для оценки как возмущающего воздействия, так и степени их нечувствительности.
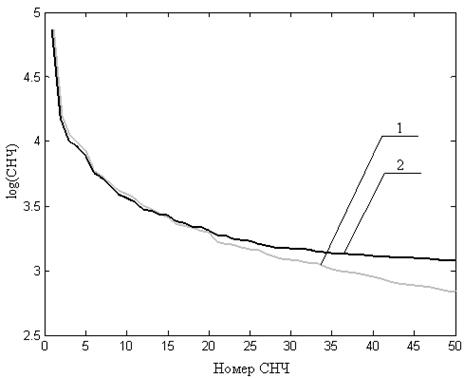
Рис.8.2. Интерполяционный сплайн, отражающий зависимость log(СНЧ) от его номера: 1 – исходное ЦИ; 2 – возмущенное мультипликативным шумом ЦИ
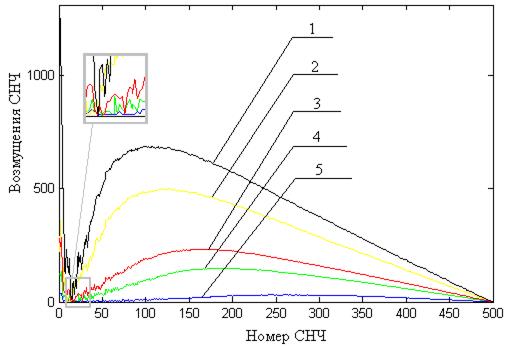
Рис.8.3. Интерполяционные сплайны первой степени, отражающие зависимость возмущений СНЧ матрицы ЦИ от номера СНЧ для различных возмущающих воздействий, смоделированных при помощи наложения шума: 1 – мультипликативного; 2 - «соль и перец»; 3 - пуассонова; 4 – гауссовского ( 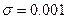 ) с нулевым матожиданием; 5 - гауссовского (
) с нулевым матожиданием; 5 - гауссовского ( 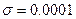 ) с нулевым матожиданием
) с нулевым матожиданием
Необходимо отметить, что конечно не всегда на практике будут СНЧ, для которых возмущение будет в точности равно нулю (хотя графики интерполяционных сплайнов для сингулярных спектров будут пересекаться). Это происходит в силу того, что в действительности графики сингулярных спектров являются дискретными, а их пересечение не обязательно будет соответствовать натуральному значению номера соответствующего СНЧ.
Дата добавления: 2016-07-22; просмотров: 2242;











