ПОСЛЕДОВАТЕЛЬНОСТЬ РАСЧЕТА КЛАССИЧЕСКИМ МЕТОДОМ

В общем случае расчет переходных процессов классическим методом включает следующие этапы:

1. Нахождение независимых начальных условий из расчета установившегося режима до коммутации.

2. Нахождение принужденной составляющей из расчета установившегося режима в послекоммутационной цепи.

3. Составление характеристического уравнения и определение его корней.

4. Запись выражения свободной составляющей в форме, определяемой видом найденных корней.

5. Определение постоянных интегрирования с помощью начальных условий и законов Кирхгофа.

6. Нахождение искомой величины как суммы принужденной и свободной составляющих.

1.5. ПРИМЕРЫ РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ

КлассическиМ методОМ

1.5.1. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ r - L ПРИ ЕЕ ПОДКЛЮЧЕНИИ

К ИСТОЧНИКУ ЭДС

Такие процессы имеют место, например, при подключении к источнику питания электромагнитов, трансформаторов, электрических двигателей и т.п.

Исходное дифференциальное уравнение, описывающее процессы в цепи на рис.1.8 после коммутации

.

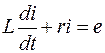Рассмотрим два случая:

а) Источник постоянной ЭДС

e(t) = E;

б) Источник синусоидальной ЭДС

e(t) = E_msin(ωt + ψ).

Согласно рассмотренной методике для тока в цепи можно записать

i(t) = i _пр (t)+i_св(t).

Независимое начальное условие 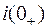для данной цепи получаем с помощью первого закона коммутации из анализа докоммутационного режима (ключ разомкнут, цепь отключена от источника энергии – следовательно, имеем нулевое начальное условие):

.

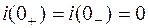Для случая а) в установившемся режиме после коммутации имеем цепь постоянного тока (сопротивление индуктивности L равно нулю). Следовательно, принужденная составляющая тока

.

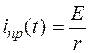Составим характеристическое уравнение:

; ; ,

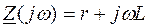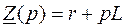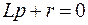откуда корень 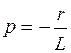и постоянная времени .

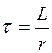Таким образом, общий вид свободной составляющей при одном корне характеристического уравнения (см. табл.1.1)

.

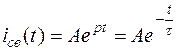Для определения постоянной интегрирования А запишем значение свободной составляющей в начальный момент времени

.

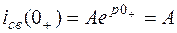Для момента времени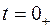

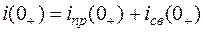
и, следовательно

.

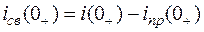Получаем постоянную интегрирования A для свободной составляющей

.

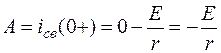Окончательное выражение для свободной составляющей тока

.

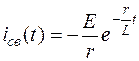Таким образом, ток в цепи в переходном процессе для случая а) описывается выражением

,

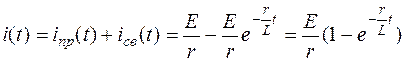а напряжение на катушке индуктивности – выражением

.

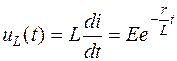Качественный вид кривых i(t) и u_L(t), соответствующих полученным решениям для случая а), представлен на рис.1.9.

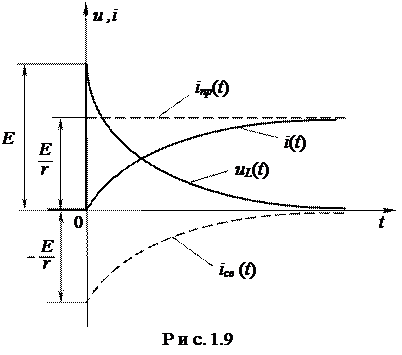Для случая б) при синусоидальном источнике питания принужденная составляющая рассчитывается с использованием символического метода:

,

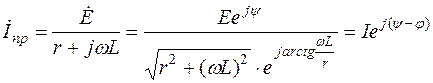где , , .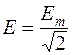

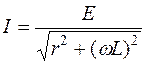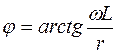Отсюда принужденная составляющая тока для случая б)

,

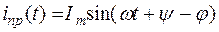где амплитудное значение тока .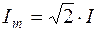

Выражение свободной составляющей в общем виде не зависит от вида источника ЭДС. Следовательно,

.

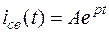Постоянная интегрирования A для свободной составляющей в этом случае

.

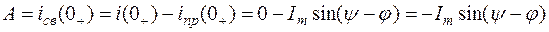Окончательное выражение для свободной составляющей тока

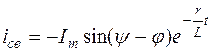
Таким образом, ток в цепи r-L в переходном процессе для случая б) описывается выражением

.

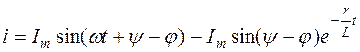Анализ полученного для случая б) выражения показывает:

1. При начальной фазе ЭДС источника 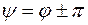постоянная интегрирования А = 0. Таким образом, в этом случае коммутация не повлечет за собой переходного процесса, и в цепи сразу возникнет установившийся режим.

2. При начальной фазе ЭДС источника 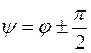свободная составляющая максимальна по модулю. В этом случае ток переходного процесса достигает своего наибольшего значения.

Качественный вид кривой i(t), соответствующей полученному решению для случая б) при 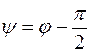, представлен на рис.1.10.

Как видно из рис.1.10, максимум тока имеет место примерно через время 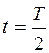после коммутации. Если постоянная времени 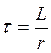значительна по величине, то за полпериода свободная составляющая существенно не уменьшается. В этом случае максимальная величина тока переходного процесса 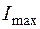может существенно превышать амплитуду тока установившегося режима I_m. В пределе при τ → ∞ максимальный ток I_max → 2I_m.