ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ ИНТЕГРИРОВАНИЯ

В каждом из приведенных в табл.1.1 случаев для нахождения свободной составляющей х_св кроме корней характеристического уравнения необходимо определить постоянные интегрирования (А_k, ψ_k). Определение постоянных интегрирования производят путем совместного решения системы линейных алгебраических уравнений по известным значениям корней характеристического уравнения, а так же по известным значениям свободной составляющей х_св и ее производных, взятых при .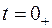

Для любой электрической цепи с помощью законов Кирхгофа и законов коммутации можно найти:

- численное значение искомой свободной составляющей х_св при : ;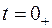

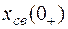- численное значение первой, а если необходимо, и высших производных от искомой свободной составляющей х_св при 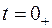: 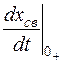, 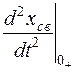и т.д.

Полагая значения этих величин, а также корней характеристического уравнения известными, рассмотрим методику определения постоянных интегрирования для наиболее характерных случаев.

1. Цепь первого порядка имеет характеристическое уравнение первой степени с одним корнем p. Выражение свободной составляющей при этом

.

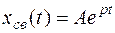Подстановка 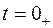дает

.

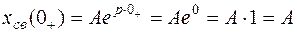Таким образом, постоянная интегрирования A в этом случае определяется по значению свободной составляющей :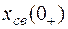

.

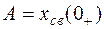2. Цепь второго порядка имеет характеристическое уравнение второй степени (квадратное уравнение) с двумя корнями.

2.1. Если корни уравнения p₁и p₂ действительные и не равны друг другу, выражение свободной составляющей имеет вид

.

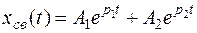В этом случае для нахождения свободной составляющей 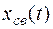необходимо определить две постоянных интегрирования А₁ и А₂. Следовательно, необходимо получить еще одно уравнение, связывающее искомые величины.

Для этого продифференцируем по времени уравнение для свободной составляющей:

.

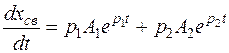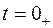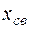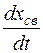Подстановка в уравнения для и дает

;

.

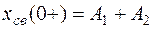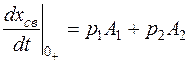Совместное решение этих уравнений дает искомые постоянные интегрирования А₁ и А₂.

2.2. Если корни уравнения p₁ = p₂ = p действительные и равные (кратные), выражение свободной составляющей имеет вид

.

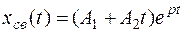В этом случае необходимо определить две постоянных интегрирования А₁ и А₂.

Продифференцируем по времени уравнение для свободной составляющей:

.

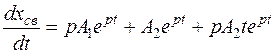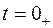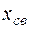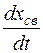Подстановка в уравнения для и дает

;

.

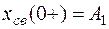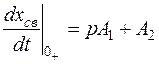Совместное решение этих уравнений дает искомые постоянные интегрирования А₁ и А₂.

2.3. Если корни характеристического уравнения p_1,2 = – δ ± jω₀комплексно-сопряженные, выражение свободной составляющей имеет вид

.

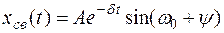Здесь δ – коэффициент затухания; ω₀ – угловая частота.

В этом случае необходимо определить две постоянных интегрирования А и ψ.

Продифференцируем по времени уравнение для свободной составляющей:

.

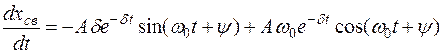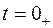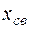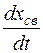Подстановка в уравнения для и дает

;

.

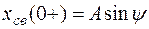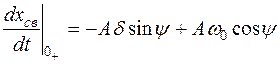Совместное решение этих уравнений дает искомые постоянные интегрирования А₁ и А₂.

Примечание. Для облегчения нахождения значения величины 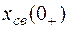и ее производной 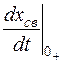рекомендуется сначала решать задачу относительно тока через индуктивность или напряжения на емкости и только затем с помощью законов Кирхгофа определять любую другую величину через найденную.