ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ

1.1. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ

При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, обрыве, колебаниях значения какого-либо параметра и т.п., в ней возникают переходные процессы.

Переходным называется процесс, возникающий в электрической цепи при переходе от одного установившегося режима работы к другому. При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые способны нарушить работу систем автоматики и других устройств, вплоть до выхода их из строя. С другой стороны, переходные процессы находят практическое применение, например, в различного рода электронных генераторах.

Переходные процессы вызываются коммутациями в цепи. Коммутация – процесс замыкания или размыкания выключателей. На схеме коммутация показывается срабатыванием ключа (рис.1.1, а – на замыкание, б – на размыкание).

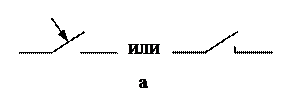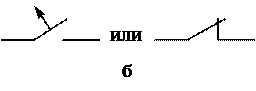Р и с. 1.1

Физически переходные процессы представляют собой процессы перехода цепи от одного энергетического состояния в докоммутационном режиме к другому энергетическому состоянию в послекоммутационном режиме, и обусловлены несоответствием запаса энергии в магнитном поле катушки и электрическом поле конденсатора до коммутации, его значению для нового состояния цепи.

Очевидно, что эти процессы не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле накопительных элементов электрической цепи.

Общий подход к расчету переходных процессов в любой электрической цепи заключается в составлении с помощью законов Кирхгофа дифференциальных уравнений, решение которых может проводиться различными методами.

Основные методы анализа переходных процессов в линейных цепях [1,2]:

1. Классический метод, заключающийся в непосредственном интегрировании дифференциальных уравнений, описывающих электромагнитное состояние цепи.

2. Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам.

3. Частотный метод,основанный на преобразовании Фурье и находящий широкое применение при решении задач синтеза.

4. Метод расчета с помощью интеграла Дюамеля, используемый при сложной форме кривой возмущающего воздействия.

5. Метод переменных состояния,представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого прядка, записанных в нормальной форме (форме Коши).

1.2. ЗАКОНЫ КОММУТАЦИИ

Допустим, что коммутация происходит в момент времени 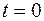и протекает мгновенно. Под 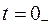будем понимать момент времени непосредственно до коммутации, а под 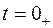- момент времени непосредственно после коммутации. На рис.1.2 это проиллюстрировано на примере изменения во времени напряжения на индуктивности и напряжения на емкости:

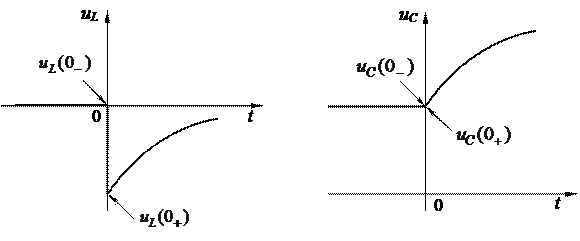Р и с. 1.2

Здесь 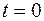– момент коммутации; 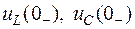– численные значения напряжений непосредственно до коммутации; 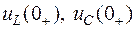– численные значения напряжений непосредственно после коммутации.

В резистивном элементе r электрическая энергия превращается в тепло и рассеивается в окружающую среду. В индуктивности накапливается энергия магнитного поля 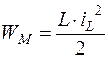, а в емкости – энергия электрического поля .

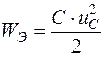При коммутации происходит изменение суммарной энергии электромагнитного поля. Процесс изменения этой энергии не может происходить мгновенно, т.к. в этом случае мощность источника энергии должна быть бесконечно большой, а таких источников не существует. Энергию электромагнитного поля можно сравнить с кинетической энергией, запасенной во вращающемся маховике - и та и другая мгновенно изменяться не может.

Поскольку энергия электромагнитного поля мгновенно изменяться не может, следовательно, не могут изменяться мгновенно обуславливающие её ток в индуктивности 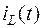и напряжение на емкости .

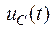Это обстоятельство определяет законы коммутации.

Первый закон коммутации: ток в ветви с индуктивности непосредственно до коммутации 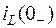равен току в ней непосредственно после коммутации :

.

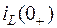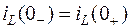Другими словами, ток в ветви с катушкой индуктивности в момент коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него (рис.1.3,а).

Упрощенно этот закон формулируют так – ток в индуктивности скачком измениться не может.

Второй закон коммутации: напряжение на конденсаторе непосредственно до коммутации 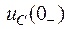равно напряжению на нем непосредственно после коммутации :

.

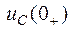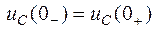Другими словами, напряжение на конденсаторе в момент коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него (рис.1.3,б).

Упрощенно этот закон формулируют так – напряжение на конденсаторе скачком измениться не может.

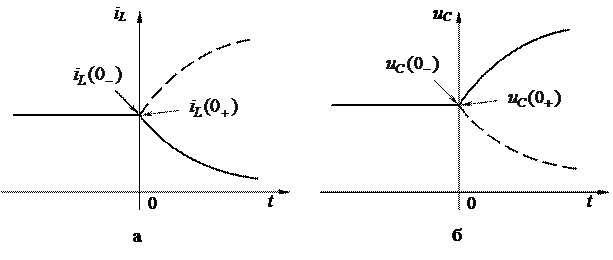Р и с. 1.3

Необходимо подчеркнуть, что ток и напряжение на резисторе (i_r, u_r), напряжение на индуктивности (u_L) и ток в ёмкости (i_C) в момент коммутации могут изменяться как угодно.

Доказать законы коммутации можно «от противного»: если допустить обратное, то получаются бесконечно большие значения 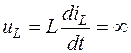и 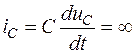, что приводит к нарушению законов Кирхгофа.

Примечание. В особых случаях (некорректные коммутации), использование законов коммутации возможно лишь в другой, обобщенной формулировке:

первый обобщенный закон коммутации: магнитный поток, сцепленный с катушками индуктивности контура, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения:

.

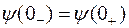второй обобщенный закон коммутации: электрический заряд на конденсаторах, присоединенных к любому узлу, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения:

.

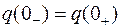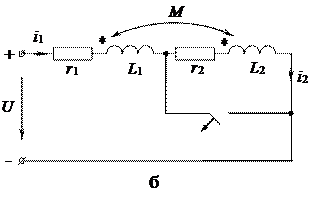В качестве иллюстрации могут служить схемы на рис.1.4, переходные процессы в которых относятся к так называемым некорректным коммутациям(название произошло от пренебрежения в подобных схемах малыми параметрами, корректный учет которых может привести к существенному усложнению задачи).

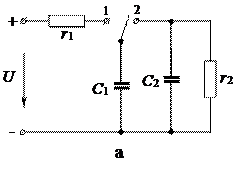Р и с. 1.4

Действительно, в схеме на рис.1.4,а при переключении ключа из положения 1 в положение 2 трактование второго закона коммутации как невозможность скачкообразного изменения напряжения на конденсаторе приводит к невыполнению второго закона Кирхгофа .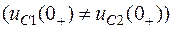

Аналогично в схеме на рис.1.4,б при размыкании ключа трактование первого закона коммутации как невозможность скачкообразного изменения тока через катушку индуктивности приводит к невыполнению первого закона Кирхгофа 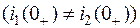. Для данных схем, исходя из сохранения заряда и соответственно потокосцепления, можно записать:

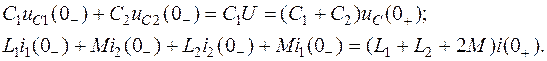
Таким образом, более общей формулировкой законов коммутации является положение о невозможности скачкообразного изменения в момент коммутации для схем с катушкой индуктивности – потокосцеплений, а для схем с конденсаторами – зарядов на них.

1.3. начальные условия

Значения токов и напряжений на элементах цепи в начальный момент времени 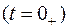называются начальными условиями.Начальные условия принято делить на независимые (основные) и зависимые (неосновные).

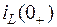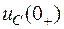К независимым начальным условиям относятся ток (потокосцепление) в катушке индуктивности и напряжение (заряд) на конденсаторе в момент коммутации. Независимые начальные условия и определяются на основании законов коммутации из расчета докоммутационного установившегося режима в цепи.

Зависимыми начальными условиями называются значения остальных токов и напряжений в начальный момент времен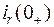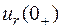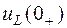и ( , , и 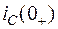), а также производных от искомой функции в момент коммутации. Они определяются по независимым начальным условиям с помощью уравнений по законам Кирхгофа, записанных для момента времени .

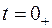Если до коммутации ток в индуктивности 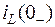и напряжение на емкости 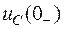равны нулю, то имеют место нулевые начальные условия: , .

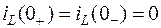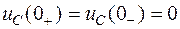В случае 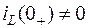и 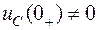имеем ненулевые начальные условия.

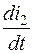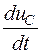Пример.В схеме на рис.1.5 определим значения токов и производных и в момент времени 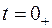при условии, что до коммутации конденсатор не заряжен.

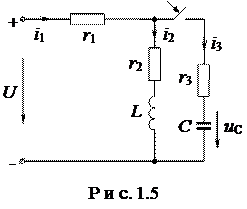В соответствии с законами коммутации независимые начальные условия

;

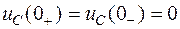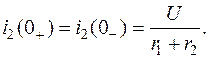
На основании второго закона Кирхгофа для начального момента времени имеем

.

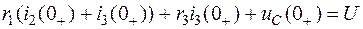Откуда получаем зависимые начальные условия

;

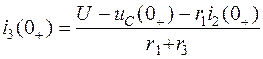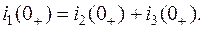
Для известных значени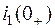й и 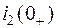из уравнения

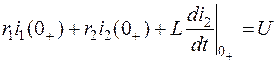
определяем значение .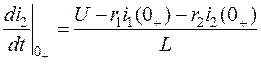

Значение производной от напряжения на конденсаторе в момент времени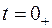

.

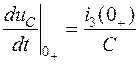1.4. Классический метод расчета ПЕРЕХОДНЫХ ПРОЦЕССОВ

ОСНОВНЫЕ ПОЛОЖЕНИЯ

Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений на участках цепи в переходном процессе.

В общем случае при использовании классического метода расчета составляются уравнения электромагнитного состояния цепи по законам Ома и Кирхгофа для мгновенных значений напряжений и токов, связанных между собой на отдельных элементах цепи соотношениями:

- резистор (идеальное активное сопротивление): ;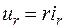

- катушка индуктивности (идеальная индуктивность): ;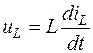

- конденсатор (идеальная емкость): , .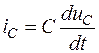

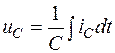Например, для последовательной цепи, содержащей линейные резистор r, катушку индуктивности L и конденсатор С (рис.1.6), при ее подключении к источнику ЭДС e по второму закону Кирхгофа имеем

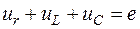
или

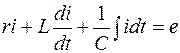. (1.1)

Подставив в (1.1) значение тока через конденсатор 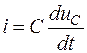, получим линейное неоднородное дифференциальное уравнение второго порядка относительно :

.

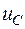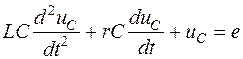В общем случае для цепи с n независимыминакопителями энергии уравнение, описывающее переходный процесс,имеет вид:

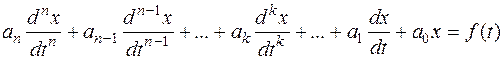, (1.2)

где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.); f (t) - известное возмущающее воздействие (напряжение и (или) ток источника электрической энергии); 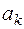- k-й постоянный коэффициент, определяемый параметрами цепи.

Порядок данного уравнения равен числу независимых накопителей энергии в послекоммутационной цепи, под которыми понимаются катушки индуктивности и конденсаторы в упрощенной схеме, получаемой после объединения индуктивностей и соответственно емкостей элементов, соединенных последовательно или параллельно.

Наличие индуктивных связей на порядок дифференциального уравнения не влияет.

В зависимости от порядка дифференциальных уравнений, описывающих исследуемую цепь, различают цепи первого, второго и более высокого порядка.

Как известно из математики, общее решение неоднородного уравнения (1.2) представляет собой сумму частного решения исходного неоднородного уравнения и общего решения однородного уравнения, получаемого из исходного путем приравнивания его левой части к нулю.

Поскольку с математической стороны не накладывается каких-либо ограничений на выбор частного решения (1.2), применительно к электротехнике в качестве последнего удобно принять решение, соответствующее искомой величине х в установившемся послекоммутационном режиме (теоретически для t → ∞).

Частное решение уравнения (1.2) определяется видом функции f (t), стоящей в его правой части, и поэтому называется принужденной составляющей (обозначается х_пр).

Для цепей с заданными постоянными или периодическими напряжениями (токами) источников принужденная составляющая определяется из расчета установившегося режима работы цепи после коммутации любым методом расчета линейных электрических цепей. Например, при синусоидальном источнике питания рекомендуется использовать символический метод расчета.

Вторая составляющая общего решения х уравнения (1.2) – решение (1.2) с нулевой правой частью – соответствует режиму, когда внешние (принуждающие) силы (источники энергии) на цепь непосредственно не воздействуют. Влияние источников проявляется здесь через энергию, запасенную в полях катушек индуктивности и конденсаторов. Данный режим работы схемы называется свободным и описывается линейным однородным дифференциальным уравнением (1.3), общее решение которого называется свободной составляющей (обозначается х_св).

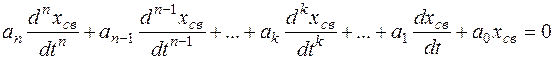. (1.3)

В соответствии с вышесказанным, общее решение уравнения (1.2) имеет вид

х = х_пр + х_св. (1.4)

Соотношение (1.4) показывает, что в классическом методе расчета послекоммутационный режим рассматривается как наложение друг на друга двух режимов – принужденного, длящегося теоретически бесконечно долго, и свободного, имеющего место только в течение переходного процесса.

Поскольку принцип наложения справедлив только для линейных систем, метод решения, основанный на указанном разложении, справедлив только для линейных цепей.

В соответствии с определением свободной составляющей х_св в ее выражение входят постоянные интегрирования, число которых равно порядку дифференциального уравнения. Постоянные интегрирования находятся из начальных условий.

Выражение свободной составляющей определяется видом корней характеристического уравнения и зависит от значений параметров схемы (r, L, C) и схемы их соединений [1,2,3].

Зависимость вида свободной составляющей от вида корней характеристического уравнения приведена в табл.1.1.

Таблица 1.1

Вид корней характеристического уравнения	Выражение для свободной составляющей
Корни p1, p2, …, pn вещественные и различные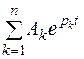
Корни p1, p2, …, pn вещественные и p1= p2= …= pm=p (m<n)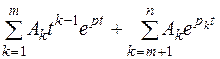
Пары комплексно-сопряженных корней pk,k+1= – δk ± jωk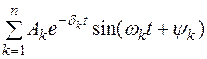

Необходимо помнить, что, поскольку с течением времени свободная составляющая затухает, вещественные части корней характеристического уравнения не могут быть положительными.

При вещественных корнях х_св монотонно затухает, и имеет место апериодический переходный процесс.Наличие пары комплексно сопряженных корней обусловливает появление затухающих синусоидальных колебаний (колебательный переходный процесс).

Важной характеристикой при исследовании переходных процессов является постоянная времени τ, определяемая для цепей первого порядка, как:

,

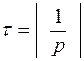где р – корень характеристического уравнения.

Постоянную времени можно интерпретировать как временной интервал, в течение которого свободная составляющая уменьшится в е раз по сравнению со своим начальным значением. Теоретически переходный процесс длится бесконечно долго, однако на практике считается, что он заканчивается при (3÷4) τ.