Внутренняя энергия реального газа. Эффект Джоуля-Томсона. Сжижение газов. Получение низких температур.

Известно, что внутренняя энергия идеального газа определяется кинетической энергией хаотического движения молекул. В случае реального газа необходимо учитывать потенциальную энергию взаимодействия молекул, которая определяется межмолекулярными Ван-дер-Ваальсовскими силами. Следовательно, внутренняя энергия реального газа определяется следующим уравнением:

(1)

Кинетическая энергия молекул пропорциональна температуре. Для одного моля газа:

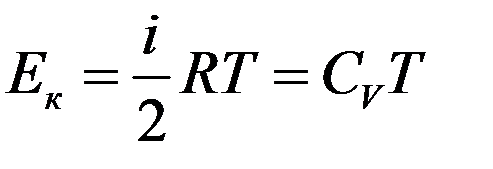(2)

где C_V – молярная теплоемкость при постоянном объеме.

Потенциальная энергия молекул зависит от расстояния между ними, поэтому она должна быть функцией объема газа. Следовательно, согласно (1), внутренняя энергия реального газа должна быть функцией двух параметров состояния: T и V.

Определим потенциальную энергию реального газа.

При расширении газа выполняется работа за счет изменения внутреннего молекулярного давления:

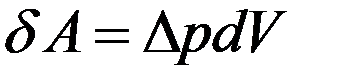(3)

где ∆p = a/V² – внутреннее молекулярное давление. Эта работа равна изменению потенциальной энергии:

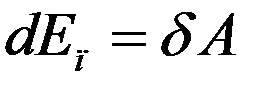(4)

Проинтегрировав (4) с учетом (3) получим потенциальную энергию реального газа:

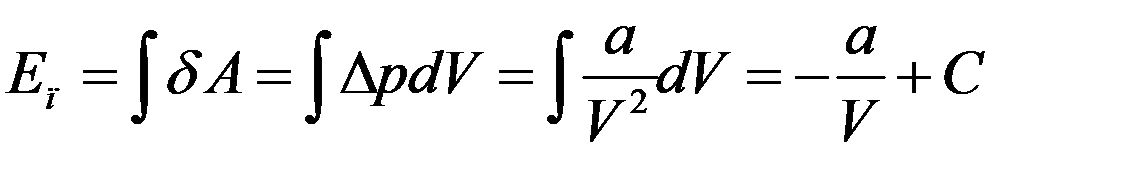(5)

Значение постоянной C необходимо выбрать таким образом, чтобы потенциальная энергия газа при V→∞ стремилась к нулю, потому что если V→∞, то реальные газы по своим свойствам приближаются к идеальным газам:

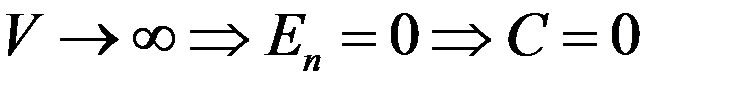
Тогда из (5) потенциальная энергия реального газа:

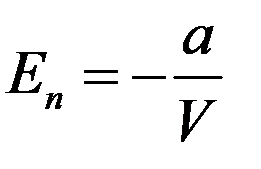(6)

С учетом (6) и (2) из (1) получим внутреннюю энергию 1 моля реального газа:

(7)

Если газ расширяется адиабатически без выполнения работы (расширение газа в пустоту), то согласно I началу термодинамики его внутренняя энергия должна оставаться постоянной:

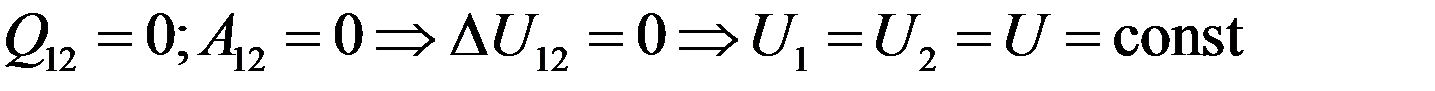
Отсюда следует, что для идеального газа:

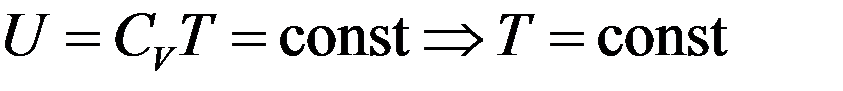
То есть температура идеального газа при расширении в пустоту не изменяется.

Для реального газа:

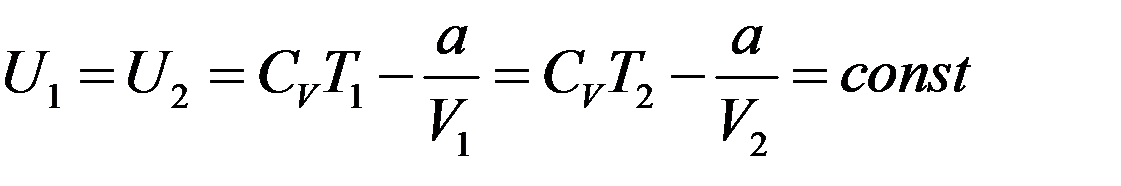
Или:

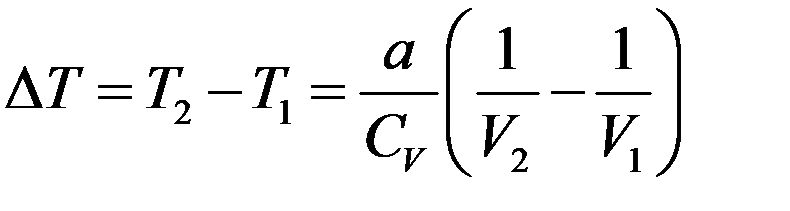(8)

Из (8) видно, что при расширении V₂ > V₁, тогда ∆T < 0, т.е. температура реального газа при расширении в пустоту уменьшается. Однако, при некоторых условиях, при расширении температура газа может и увеличиваться.

Впервые явление изменения температуры при расширении газа было исследовано Джоулем и Томсоном (рис.1).

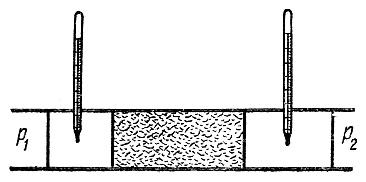
Рис.1. Схема опыта Джоуля-Томсона

Сосуды с газом соединены теплоизолированной трубкой. В трубке находится пористая перегородка (керамика, вата и т.д.). По обе стороны от перегородки установлены термометры. Пусть p₁ > p₂. Процесс расширения газа адиабатный (трубка теплоизолирована). Гидродинамическое сопротивление перегородки приводит к тому, что газ выходит из перегородки при более низком давлении, чем давление при входе. При этом газ расширяется, или, как говорят, дросселируется.

Дросселем называется любое приспособление, которое создает сопротивление протеканию газа (например, вместо керамики узкое отверстие).

Чтобы течение газа через перегородку было стационарным, используется компрессор, поддерживающий разность давлений постоянной.

Явление изменения температуры газа при его адиабатном расширении дросселированием называется эффектом Джоуля-Томсона. Опытным путем установлено, что для большинства газов при комнатных температурах ∆T < 0 – газы при расширении охлаждаются. Однако для некоторых газов (водород, гелий) ∆T > 0 – газы при расширении нагреваются.

Охлаждение газа при расширении называется положительным, а нагревание отрицательным эффектом Джоуля-Томсона.

Определим условия, от которых зависит знак эффекта (рис.2).

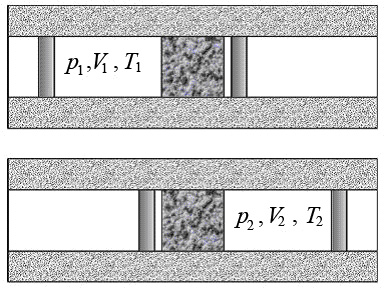
Рис.2. Расширение газа при прохождении пористой перегородки

Выделим слева от перегородки некоторый объем газа V₁. После прохождения газом перегородки его объем станет V₂. Газ расширяется адиабатно, поэтому согласно I началу термодинамики изменение внутренней энергии газа равно работе, выполненной им:

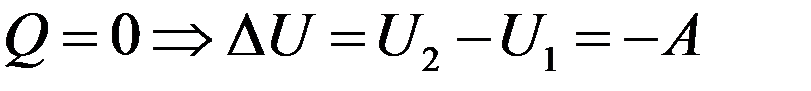(9)

Определим величину работы. Слева работу над выделенным объемом газа выполняет остальной газ из первого сосуда:

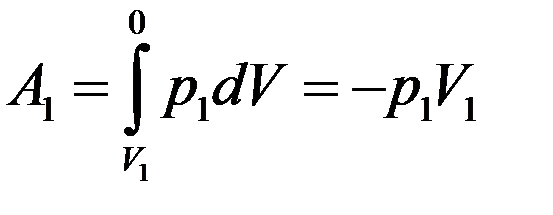(10)

Знак « - » показывает, что работа выполняется над газом. Справа, газ, расширяясь, сам, выполняет работу над остальным газом во втором сосуде:

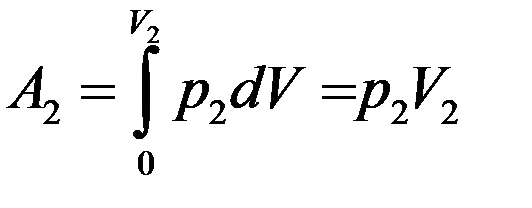(11)

Работа, выполненная газом:

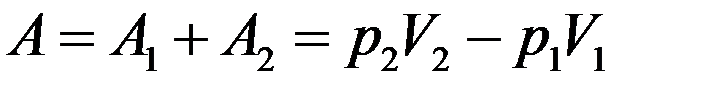(12)

С учетом (12) найдем изменение внутренней энергии газа из (9):

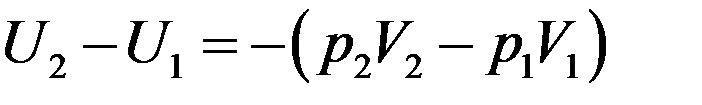
Раскрыв скобки получим:

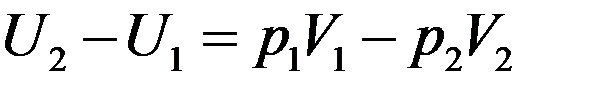(13)

Или:

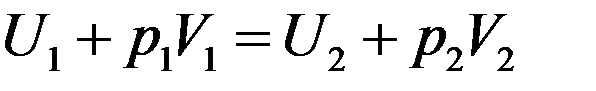(14)

Известно, что U + pV = I – энтальпия. Из (14) видно, что эффект Джоуля-Томсона протекает при постоянной энтальпии.

Для идеального газа и внутренняя энергия и произведение pV зависят только от температуры. Поэтому и энтальпия I зависит только от температуры. Из равенства энтальпий по обе стороны от перегородки вытекает и равенство температур по обе стороны перегородки для идеального газа. Поэтому для идеального газа эффект Джоуля-Томсона равен нулю ∆T = 0.

У реальных газов внутренняя энергия зависит не только от температуры, но и от объема (7). Поэтому равенство энтальпий (14) еще не свидетельствует о равенстве температур по обе стороны перегородки.

Для газов, которые подчиняются уравнению Ван-дер-Ваальса, знак эффекта Джоуля-Томсона должен зависеть от того, какая из постоянных a или b играет в уравнении большую роль.

Рассмотрим два граничных случая:

1). Пусть молекулы обладают собственным объемом, но не взаимодействуют между собой (a = 0). Тогда:

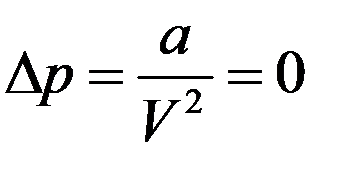
С учетом этого уравнение Ван-дер-Ваальса для одного моля газа принимает вид:

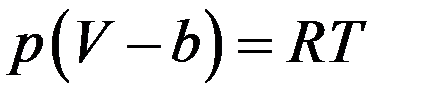
Или:

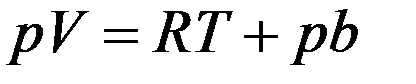(15)

Подставим (15) в (13):

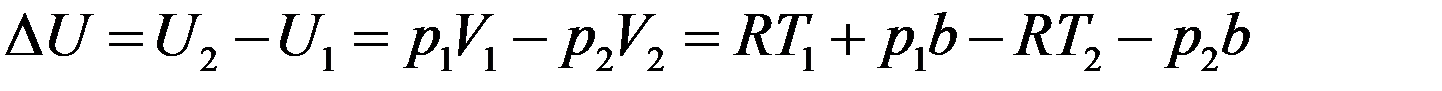
Или:

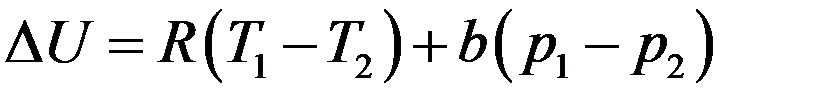(16)

С другой стороны с учетом (7):

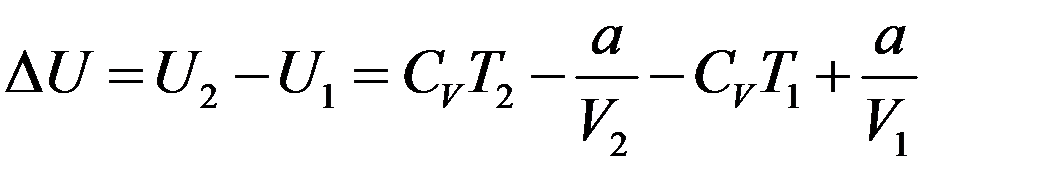
Но a = 0, тогда:

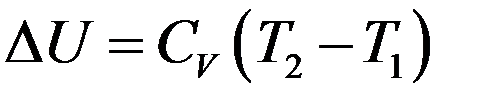(17)

Приравнивая (16) и (17) получим:

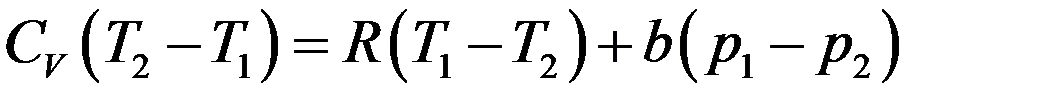
Преобразуем последнее равенство:

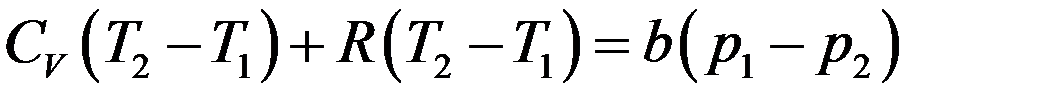
Или:

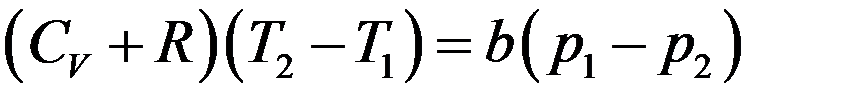
Окончательно:

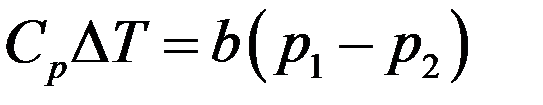(18)

Из (18) следует, что при расширении p₁ > p₂, тогда ∆T > 0 и T₂ > T₁. Следовательно, если собственный объем молекул играет большую роль, чем их взаимодействие (силы отталкивания больше сил притяжения), то температура газа после расширения повышается – эффект отрицательный.

2). Пусть на собственный объем молекул можно не обращать внимания, но их взаимодействие (притяжение) не равно нулю. Тогда в уравнении Ван-дер-Ваальса b = 0 и для одного моля газа оно принимает следующий вид:

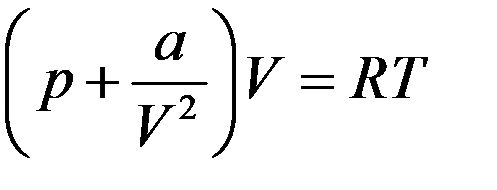
Преобразуем последнее уравнение (раскроем скобки):

(19)

Подставим (19) в (13):

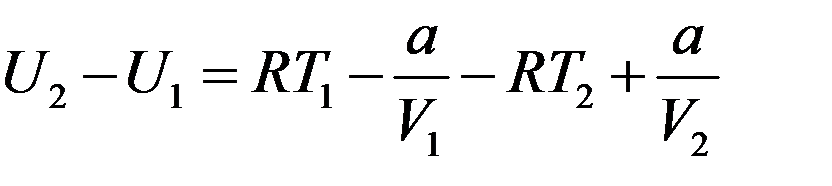(20)

Из (7) следует:

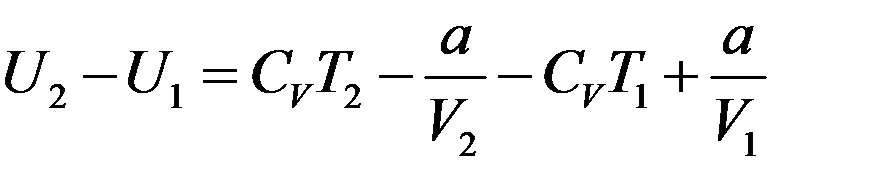(21)

Приравняем (20) и (21):

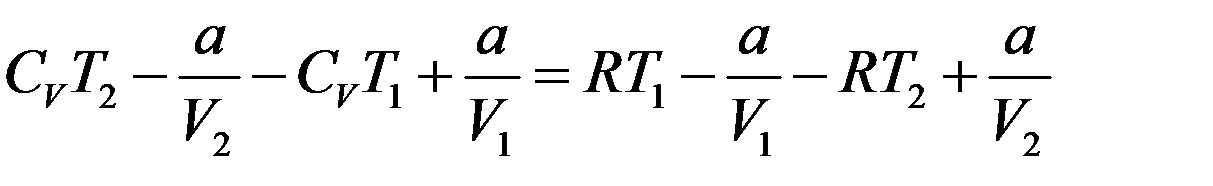
Перегруппируем члены:

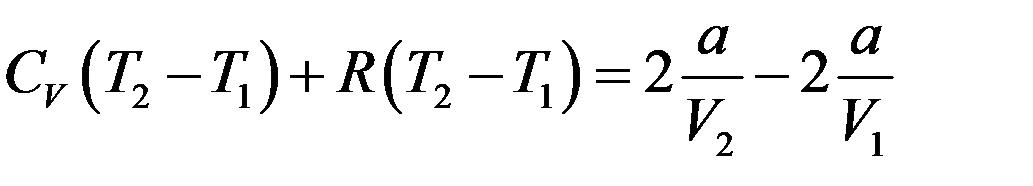
Или:

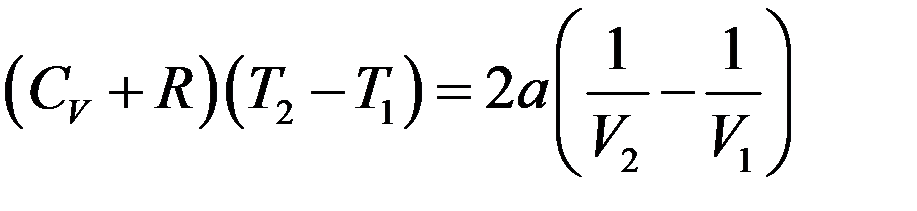
Окончательно получим:

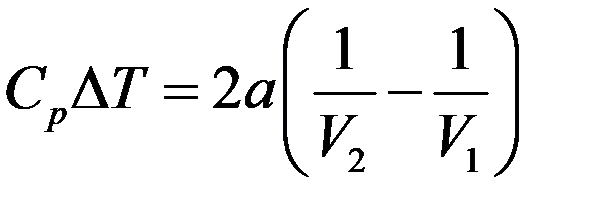(22)

Из (22) следует, что при расширении V₂ > V₁, поэтому ∆T < 0 и T₂ < T₁ – газ при расширении охлаждается. Следовательно, если взаимодействие молекул играет большую роль, чем их собственный объем (силы притяжения больше сил отталкивания), то газ при расширении охлаждается – эффект положительный.

Рассмотрим общий случай, когда надо учитывать как взаимодействие молекул, так и их собственный объем.

Пусть после расширения 1 моля газа его объем V₂ очень большой, поэтому его можно считать идеальным. Тогда согласно уравнению Клапейрона-Менделеева и уравнению (2):

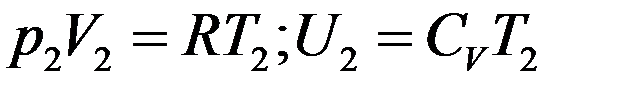(23)

Определим левую часть уравнения (14). Согласно (7):

(24)

Запишем уравнение Ван-дер-Ваальса для одного моля газа:

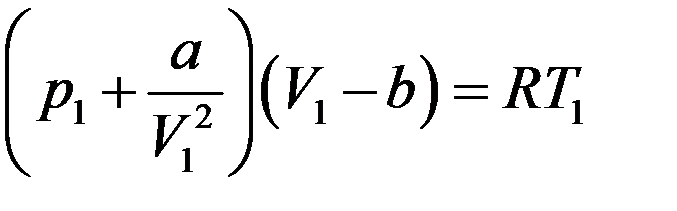
Преобразуем его:

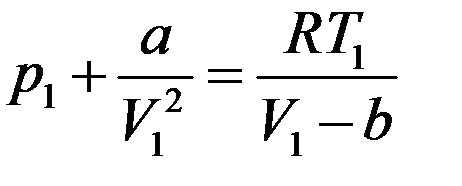
Или:

Умножим левую и правую часть последнего равенства на V₁:

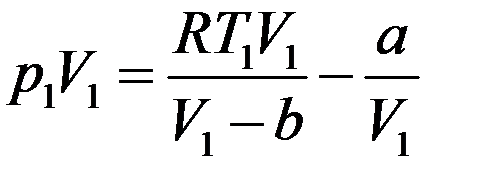(25)

Преобразуем первое слагаемое справа в (25):

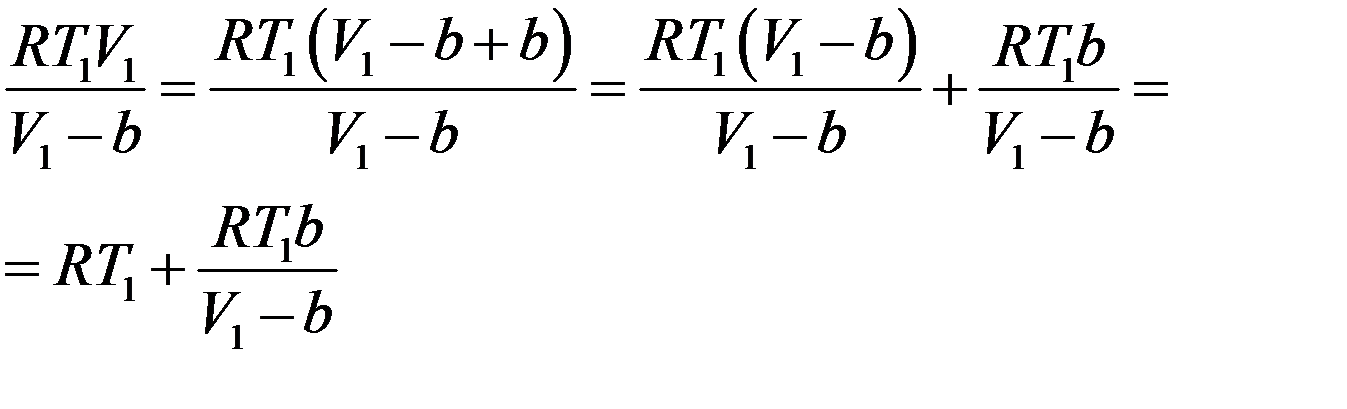(26)

Подставим (26) в (25):

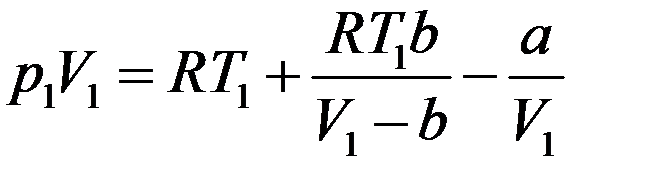(27)

Подставим (23), (24) и (27) в (14):

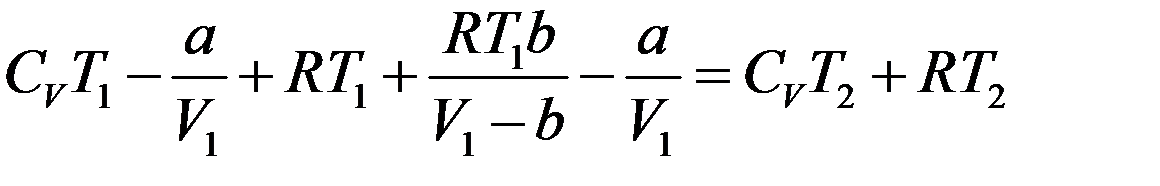
Или:

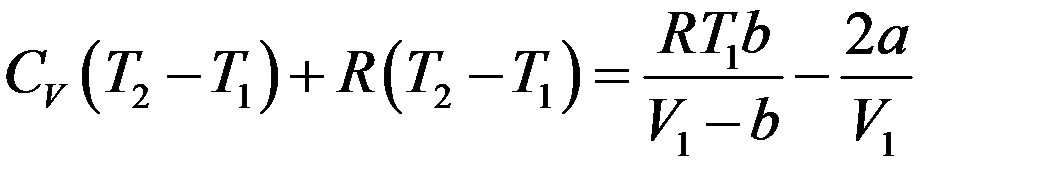
Или:

Окончательно получим:

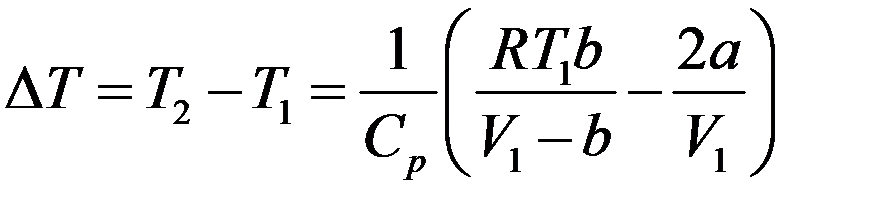(28)

Знак ∆T определяется знаком выражения в скобках. Нулевой эффект (∆T = 0) будет наблюдаться, если:

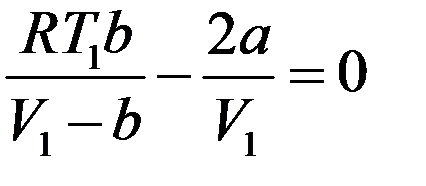
Или:

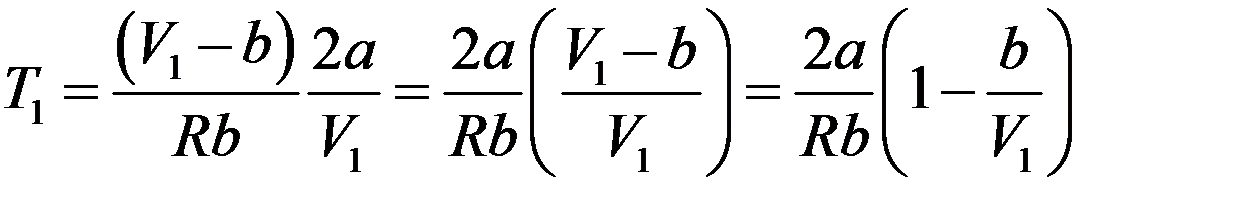
Этому уравнению соответствует кривая T₁ = f(V₁), точки которой определяют значение параметров T₁ и V₁ (начальных параметров), при которых ∆T = 0 (рис.3).

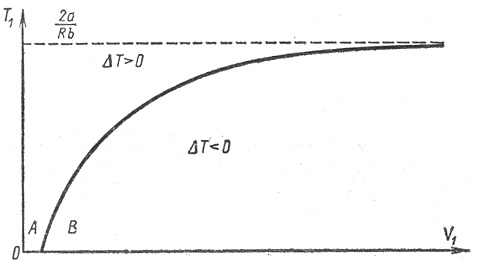
Рис.3. Области эффекта Джоуля-Томсона

Точки, которые лежат выше кривой, определяют значения T₁ и V₁, при которых ∆T > 0 и эффект отрицательный. Точки, лежащие ниже кривой определяют значения начальных параметров, при которых ∆T < 0 и эффект положительный. При больших значениях V₁, (V₁ → ∞), кривая асимптотически стремится к значению:

Это наибольшее значение температуры, при которой возможно изменение знака эффекта – называется температурой инверсии. Выше этой температуры эффект всегда отрицательный. Точки самой кривой соответствуют температуре, при переходе через которую, знак эффекта изменяется. Эта кривая называется кривой инверсии.

Из графика видно, что если расширение газа происходит при малых начальных объемах (V₁), то эффект будет отрицательным даже при низких начальных температурах – область А. Увеличение начального объема – область В изменяет знак эффекта и газ будет охлаждаться при расширении.

Температуры инверсии некоторых газов: H₂ – 192,7 K, O₂ – 1063 K, He – 40 K.

Эффект Джоуля-Томсона используется в технике для сжижения газов.

Для того чтобы перевести газ в жидкое состояние, его необходимо охладить до температуры ниже критической. Это можно сделать разными способами.

Метод Линде: 1895 год (рис.4).

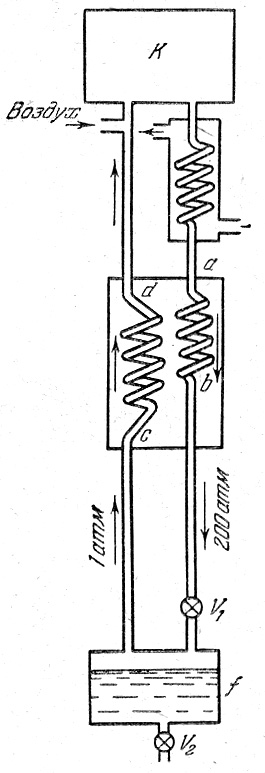
Рис.4. Схема машины Линде

Сжатый компрессором K газ проходит через змеевик, охлаждаемый проточной водой, где отдает тепло, выделившееся при сжатии. Затем газ проходит через змеевик a - b теплообменника к дроссельному вентилю V₁. При дросселировании газ резко расширяется и при этом охлаждается (эффект Джоуля-Томсона).

После первого расширения температура газа понижается недостаточно для сжижения, и, поэтому газ возвращают обратно в компрессор через змеевик c - d теплообменника, где он охлаждает перед дросселированием идущую навстречу порцию газа. Теплообменник представляет собой две трубки, вставленные одна в другую и изогнутые в виде змеевика. По внутренней трубке газ идет к дросселю, по внешней трубке навстречу движется охлажденный после дросселирования газ.

В процессе работы установки температура газа постоянно уменьшается и становится ниже критичной. Газ конденсируется и собирается в приемнике f. Та часть газа, которая не сконденсировалась, возвращается в компрессор и т.д. Этот способ сжижения газа требует много энергии.

Позднее были разработаны другие, более экономичные способы сжижения газов. В машине Клода (1902 год) (рис.5) используется как способ охлаждения газа при дросселировании, так и способ охлаждения газа при адиабатном его расширении с выполнением работы.

Приспособление, в котором газ, расширяясь, выполняет работу и за счет этого охлаждается, называется детандером. Простейший детандер – цилиндр с поршнем. Капица в качестве детандера применил турбину, которая приводилась во вращение газом, сжатым компрессором – турбодетандер. Работу, которую выполняет сжатый газ в детандере, используют для облегчения работы компрессора.

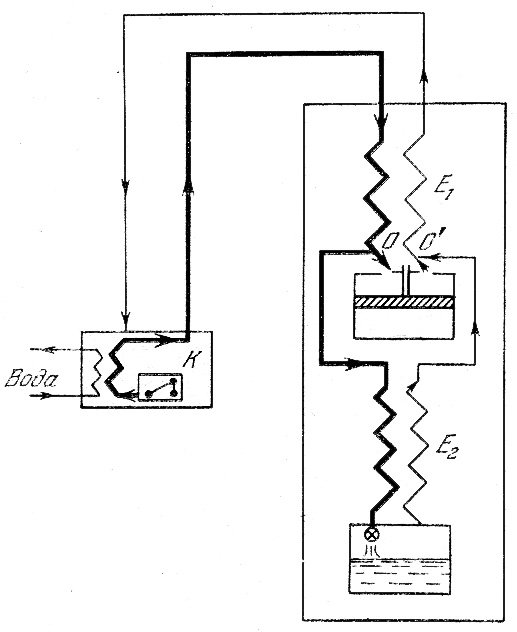
Рис.5. Схема машины Клода

Газ, сжатый компрессором, охлаждается проточной водой и проходит через теплообменник E₁, где он разделяется на два потока. Первый поток проходит через дроссель и охлаждается благодаря эффекту Джоуля-Томсона. Второй поток (~ 80% всего газа) поступает в детандер, расширяется в нем, совершая работу, и за счет этого охлаждается.

После детандера охлажденный газ возвращается в теплообменник E₁, где охлаждает встречную порцию газа, сжатого компрессором. К этому потоку газа в точке O′ присоединяется газ, охлажденный в результате дросселирования. До этого, проходя через теплообменник E₂, он также охлаждал встречный газовый поток.

Из схемы машины Клода видно, что газ, охлажденный в детандере, используется для предварительного охлаждения газа перед дросселированием. Турбодетандеры при небольших размерах обладают большой производительностью. КПД ~ 17%, на получение 1кг жидкого газа уходит ~ 1,1 кВт/час энергии.

Понятие низкой температуры относительное. Оно определяется областью явлений, которые рассматриваются при разных температурах. Для получения низких температур используют следующие методы: испарение жидких газов; эффект Джоуля-Томсона; адиабатичное расширение газа с выполнением работы.

Температура кипения жидкого газа зависит от давления пара над ним. Имея в распоряжении сжиженный газ, можно получить низкие температуры, принуждая кипеть его при пониженном давлении. Большой интерес представляет получение сверхнизких температур, лежащих ниже температуры кипения жидкого гелия (4K). Понижая давление над жидким гелием He⁴ (откачивание паров) можно получить температуру ~ 0,72K. Откачивая пары He³ можно достичь температуры ~ 0,3K – граница данного метода.

Для получения сверхнизких температур используют метод адиабатного размагничивания парамагнитных солей. Он основан на зависимости энтропии парамагнитной соли от напряженности магнитного поля.

Атомы парамагнитного вещества обладают магнитными моментами. В обычных условиях эти магнитные моменты ориентированы беспорядочно из-за теплового движения, в котором участвуют молекулы соли (рис.6,а):

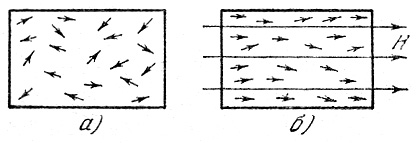
Рис.6. Ориентация магнитных моментов молекул парамагнитной соли

Если такую соль поместить в сильное магнитное поле, то магнитные моменты будут ориентироваться вдоль поля (рис.6,б). Этот процесс называется намагничиванием. Следовательно, магнитное поле приводит к тому, что степень беспорядка (магнитного) уменьшается. Поэтому уменьшается и связанная с ним энтропия.

Парамагнитную соль охлаждают жидким гелием до ~ 1K и намагничивают. После этого намагниченную, охлажденную соль изолируют от жидкого гелия и адиабатно размагничивают, удаляя из магнитного поля.

При адиабатическом процессе:

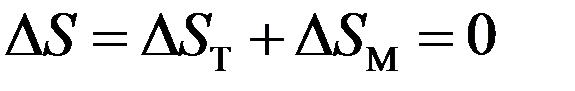
где ∆S_T – изменение энтропии, обусловленное тепловым движением молекул (температурой), ∆S_M – изменение энтропии, обусловленное магнитными свойствами.

При адиабатном размагничивании ∆S_M > 0 – энтропия, обусловленная магнитными свойствами, возрастает, потому что магнитные моменты молекул в отсутствие магнитного поля ориентируются беспорядочно (рис.6,а). Следовательно, при этом должна уменьшиться энтропия, связанная с тепловым движением (температурой) ∆S_T < 0. Поэтому температура парамагнитной соли уменьшится. Используя этот метод можно получить температуры ~ 10^-5K.

При низких температурах резко изменяются физические свойства вещества (сверхпроводимость, сверхтекучесть и т.д.).

Лекция 18

Фазовые переходы I рода. Равновесие жидкости и пара. Свойства насыщенного пара. Уравнение Клапейрона-Клаузиуса. Понятие о фазовых переходах II рода. Влажность воздуха. Особенности фазовых переходов воды и их роль в природе.

Фазой называется равновесное состояние вещества, которое по своим физическим свойствам отличается от других возможных равновесных состояний этого вещества.

Если система состоит из одного однородного вещества, то она однофазная. Во многих случаях система может состоять из нескольких разных однородных частей одного и того же вещества – такая система называется многофазной.

Разными фазами являются разные агрегатные состояния вещества, например: пар, вода и лед – разные фазы воды.

Процессы, при которых вещество переходит из одной фазы в другую, при изменении внешних условий (температура, давление и т.д.) называются фазовыми переходами.

Фазовый переход жидкости в газообразное состояние называется парообразованием. Обратный переход из газообразного состояния в жидкое называется конденсацией. Парообразование происходит при испарении и кипении.

Испарением называется парообразование, которое происходит с поверхности жидкости при любой температуре. Интенсивность испарения зависит от рода жидкости, температура, площади поверхности жидкости, наличия потоков воздуха.

При испарении жидкость покидают наиболее быстрые молекулы, которые могут преодолеть силу притяжения со стороны остальных молекул жидкости. Кроме того, они должны выполнить работу против внешнего давления пара, который существует над жидкостью. Очевидно, что эта работа выполняется за счет кинетической энергии самих молекул.

Поэтому жидкость покидают самые «быстрые» молекулы. Следовательно, средняя кинетическая энергия молекул оставшихся в жидкости уменьшается, и жидкость при испарении охлаждается (спирт, эфир на коже человека). Чтобы при испарении температура жидкости не уменьшалась ей необходимо передавать некоторое количество теплоты (энергию).

Количество теплоты, которое необходимо передать единице массы жидкости для изотермического перевода ее в пар при внешнем давлении равном давлению насыщенного пара при данной температуре называется удельной теплотой парообразования.

Она зависит от рода жидкости и температуры. Процесс парообразования сильно зависит от давления, под которым находится жидкость. Пока давление насыщенного пара при данной температуре меньше внешнего, испарение происходит медленно, спокойно.

При некоторой температуре начинается бурный процесс парообразования – кипение жидкости. Оно характеризуется возникновением пузырьков пара внутри жидкости, которые увеличиваются, поднимаясь к поверхности жидкости, перемешивая ее.

Температура кипения это и есть та температура, при которой давление насыщенного пара равно внешнему давлению. Температура кипения зависит от рода жидкости, внешнего давления, наличия примесей.

Молекулы жидкости, которые покинули ее, могут вернуться обратно. Это значит, что процессы парообразования и конденсации происходят одновременно. Обратный испарению процесс конденсации сопровождается выделением теплоты, такой же, которая была затрачена на испарение.

Если количество молекул, покидающих жидкость и возвращающихся в нее за какой-то промежуток времени одинаковое, то количество жидкости и пара при данной температуре изменяться не будет. Имеет место динамическое равновесие.

Пар, который находится в динамическом равновесии со своей жидкостью, называется насыщенным паром.

В отличие от газов давление и плотность насыщенного пара не зависит от объема. Поэтому на экспериментальных изотермах Ван-дер-Ваальса наблюдаются горизонтальные участки.

При повышении температуры (при V = const) плотность насыщенного пара увеличивается, а плотность жидкости уменьшается (рис.1).

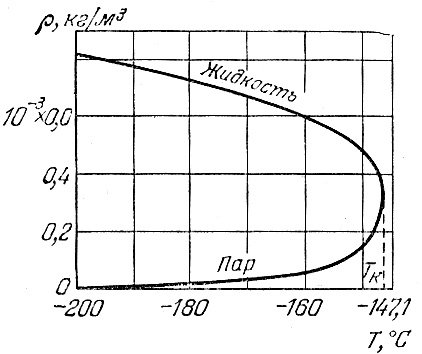
Рис.1. Зависимости плотности жидкого азота и его насыщенного пара от температуры.

Плотность жидкости и плотность насыщенного пара достигают одинакового значения при критической температуре. В этой точке у этих кривых общая касательная (вертикаль).

При повышении температуры увеличивается плотность насыщенного пара, следовательно, увеличивается и его давление (рис.2).

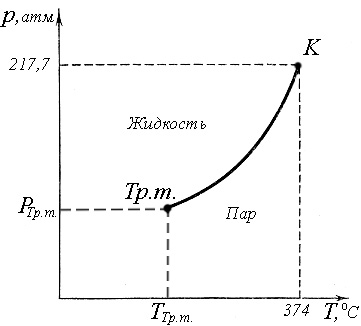
Рис.2. Зависимость давления насыщенного пара от температуры для воды

Кривая p(T) начинается в тройной точке и заканчивается в критической точке. Как видно из графика p(T) равновесие двух фаз пар – жидкость может существовать только в некотором интервале температур и давлений. Очевидно, что кривая зависимости давления насыщенного пара от температуры совпадает с кривой зависимости температуры кипения от давления. При давлении 3570 мм.рт.ст. (~5 атмосфер) вода кипит при 150 ^oC, а при давлении 4 мм.рт.ст. при 0 ^oC.

Две любые фазы вещества могут находиться в равновесии только при определенном давлении и температуре. Определим связь между этими параметрами. Рассмотрим цикл Карно для системы состоящей из двух фаз вещества, находящихся в равновесии при температуре T и давлении p, например: жидкость - насыщенный пар (рис.3):

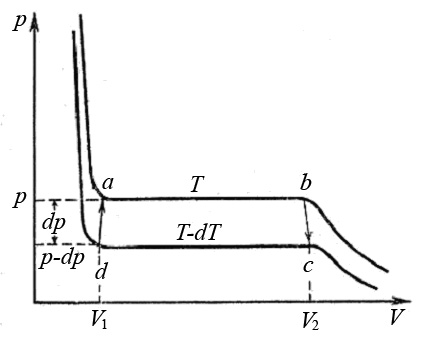
Рис.3. Цикл Карно для двухфазной системы жидкость - насыщенный пар

Изотермический процесс a – b сопровождается фазовым переходом некоторой массы жидкости m в пар. При этом переходе объем вещества увеличивается на величину ∆V:

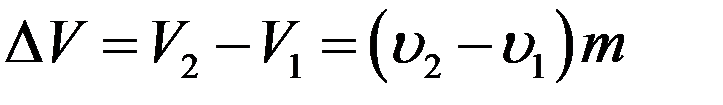(1)

где υ₁ и υ ₂ - удельные объемы жидкости и пара соответственно.

Для перехода жидкости в пар ей требуется передать количество теплоты Q₁:

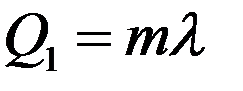(2)

где λ – удельная теплота парообразования.

Это теплоту система получает от нагревателя с температурой T при выполнении цикла Карно. КПД цикла Карно не зависит от рода рабочего тела и определяется следующим образом:

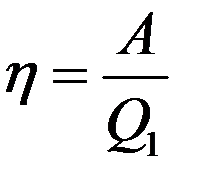(3)

где A – работа, выполненная за цикл, Q₁ – количество теплоты, полученное от нагревателя.

Работа, выполненная за цикл равна площади фигуры abcd:

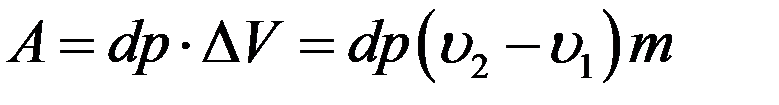(4)

Учитывая (4) и (2) из (3) получим:

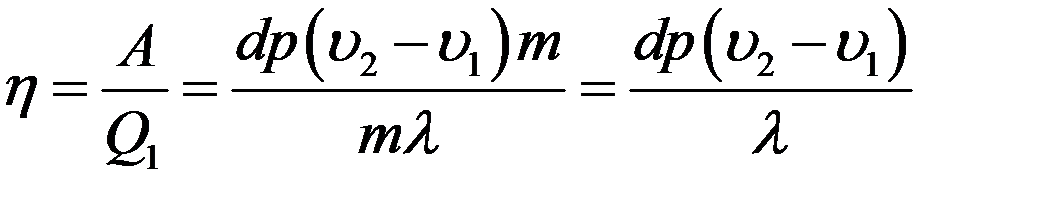(5)

С другой стороны КПД цикла Карно:

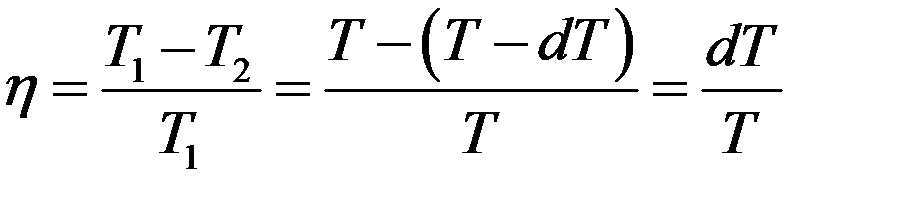(6)

Приравняем (5) и (6):

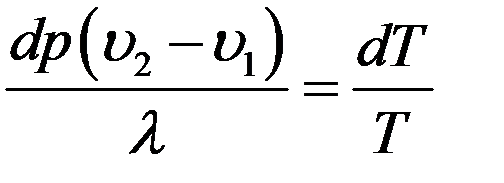
Или:

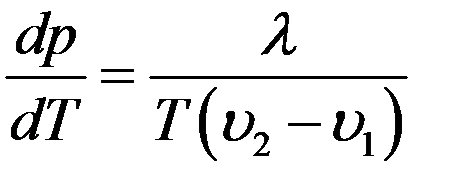(7)

Уравнение (7) – это уравнение Клапейрона – Клаузиуса. Это уравнение справедливо для всех фазовых переходов (плавление – кристаллизация, сублимация – конденсация). Оно показывает изменение давления, при котором фазы находятся в равновесии, при изменении температуры.

Знак производной dp/dT зависит от того, каким изменением удельного объема (увеличением или уменьшением) сопровождается фазовый переход, который происходит при поглощении теплоты. При испарении жидкости или твердого тела (сублимация или возгонка) удельный объем газовой фазы всегда больше чем жидкой или твердой υ₂ > υ₁, поэтому dp/dT > 0 для кривой испарения или сублимации. Повышение температуры приводит к увеличению равновесного давления и наоборот.

Определим зависимость давления насыщенного пара от температуры. При достаточно низких температурах плотность насыщенного пара мала и он ведет себя подобно идеальному газу. Запишем уравнение Клапейрона-Менделеева для 1 моля пара:

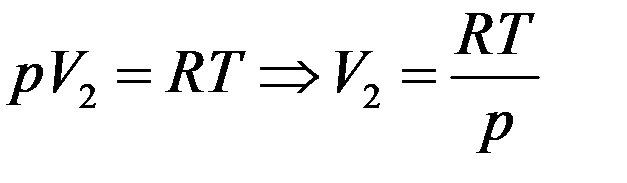(8)

При низких температурах V₁ < V₂ т.е., объем конденсированной фазы мал по сравнению с газовой. Поэтому можно положить V₁ ≈ 0. Тогда с учетом (8) из (7) получим:

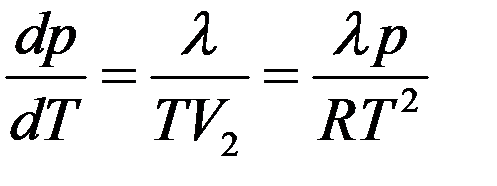(9)

Разделим переменные в (9):

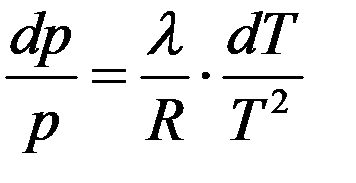(10)

Интегрируя (10) получим:

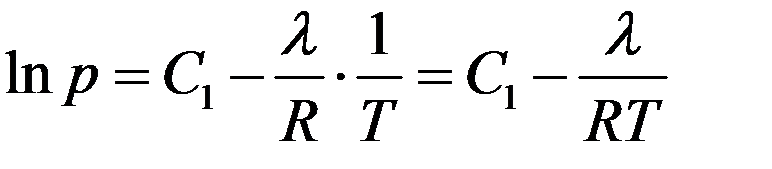(11)

где C₁ – постоянная интегрирования.

Из (11) найдем p:

(12)

где C = 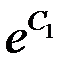- некоторая постоянная.

Из (12) следует, что давление насыщенного пара быстро возрастает с увеличением температуры.

Фазовые переходы – плавление, парообразование, сублимация и обратные им, которые происходят со скачкообразным изменением свойств вещества: внутренней энергии, энтропии, объема и других величин, – называются фазовыми переходами I рода.

При этих переходах изменяется характер упаковки частиц – дальний порядок, ближний порядок, полный беспорядок. Для фазовых переходов I рода характерно скачкообразное (в узком температурном интервале) изменение свойств вещества. Эти переходы происходят квазистатично при постоянной температуре и давлении. Поэтому можно говорить об определенной температуре фазового перехода (температура плавления, кипения и т.д.).

Однако существуют еще и фазовые переходы, при которых изменение свойств вещества происходит сразу во всем объеме в результате изменения кристаллической решетки. При этом при некоторой температуре изменяется симметрия кристаллической решетки. Эта температура и будет температурой (точкой) фазового перехода, который в данном случае называется фазовым переходом II рода.

Температура, при которой наблюдается фазовый переход II рода, называется точкой (температурой) Кюри, по имени Пьера Кюри, который открыл фазовый переход II рода в ферромагнетиках.

При таких фазовых переходах в точке перехода не будет равновесия двух фаз, потому что фазовый переход происходит одновременно во всем объеме вещества. Поэтому в точке перехода нет и скачка внутренней энергии U. Следовательно, такие переходы не сопровождаются выделением или поглощением теплоты перехода.

Однако при температурах выше и ниже точки фазового перехода вещество находится в разных кристаллических модификациях, теплоемкость которых неодинаковая.

Таким образом, в точке фазового перехода II рода скачком изменяется теплоемкость С, т.е. первая производная внутренней энергии по температуре:

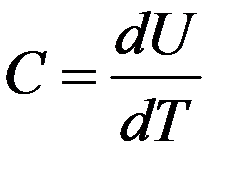
На кривой зависимости C(T) в некоторой точке при температуре равной температуре фазового перехода величина теплоемкости изменяется скачком: резко уменьшается, а затем возрастает (рис.4):

Рис.4. Лямбда – точка гелия

Форма кривой C(T) напоминает греческую букву λ, поэтому эту точку, в которой происходит фазовый переход, часто называют λ - точкой.

Примеры фазовых переходов II рода: переход ферромагнетика в парамагнетик, переход сегнетоэлектрика из полярной фазы в неполярную фазу (параэлектрическая фаза), переход жидкого гелия из состояния He I в сверхтекучее состояние He II.

При фазовых переходах II рода агрегатное состояние вещества (в отличие от фазовых переходов I рода) не изменяется.

В воздухе всегда содержится некоторое количество водяных паров. Наличие водяных паров в атмосфере имеет большое значение для жизни растений, животных и человека.

Для характеристики содержания водяных паров в воздухе вводится понятие влажности.

Количество водяного пара, находящегося в единице объема воздуха называется абсолютной влажностью.

Парциальное давление водяного пара, находящегося в воздухе называется упругостью водяного пара.

Относительной влажностью воздуха называется отношение давления водяного пара p, который находится в воздухе, к давлению насыщенного водяного пара p₀ при той же температуре:

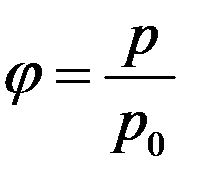
Так как давление пара (газа) пропорционально его плотности, то можно дать другое определение относительной влажности.

Относительная влажность воздуха есть отношение плотности водяного пара, находящегося в воздухе, к плотности насыщенного водяного пара при той же температуре.

Температура, при которой водяной пар, находящийся в воздухе становится насыщенным (т.е. относительная влажность становится равной 100%), называется точкой росы.

Влажность воздуха измеряется гигрометрами и психрометрами.

Вода – одна из самых интересных жидкостей. Удельная теплота парообразования воды 2,26*10⁶ Дж/кг – одна из самых больших среди подобных величин. При конденсации пара такое же количество теплоты выделяется. Испарение воды людьми, животными, растениями требует большого количества теплоты, поэтому организмы не перегреваются. При понижении температуры водяной пар становится насыщенным, при этом выпадает роса. При конденсации пара в жидкость выделяется большое количество теплоты, и температура воздуха понижается не очень резко. При возможности заморозков растения поливают, увеличивая влажность воздуха над землей с целью защиты растений от заморозков.

Очень интересным является и другой фазовый переход: плавление льда и кристаллизация воды. Удельная теплота плавления льда одна из самых больших – 3,34*10⁵ Дж/кг. Поэтому при переходе воды в лед выделяется очень большое количество теплоты, смягчающее климат в прибрежных районах. И, наоборот, при плавлении льда такое же количество теплоты поглощается, что приводит также к смягчению климата (так называемый морской климат, без резких колебаний температуры).

Плотность льда меньше плотности воды и лед плавает на поверхности воды. Теплопроводность льда маленькая. Плотность воды максимальна при 4^oC. Поэтому глубокие водоемы не промерзают зимой до дна, что очень важно для жизнедеятельности живых организмов.

Лекция 19