I.7.4 РЕЛЯТИВИСТСКИЕ ЭФФЕКТЫ
К наиболее распространённым релятивистским эффектам относятся: сокращение длины и замедление времени. Это одно из важнейших следствий, которое вытекает из лоренцева преобразования.
А. Сокращение длины
Линейные размеры тел в движущейся системе отсчёта сокращаются. При этом сокращаются продольные размеры тела (измеряемые вдоль направления движения). Поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчёта. Такое сокращение размеров называют лоренцевым сокращением.
Пусть стержень 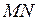 движется вместе с системой отсчёта
движется вместе с системой отсчёта 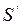 относительно системы
относительно системы  так, как показано на рисунке 44. Длина стержня измеренная в системе
так, как показано на рисунке 44. Длина стержня измеренная в системе 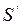 равна
равна 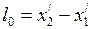 .
.
Длина тела в системе отсчёта, где оно покоится ( 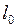 ), называется собственной длиной. Для определения длины (
), называется собственной длиной. Для определения длины ( 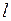 ) движущегося стержня в системе
) движущегося стержня в системе  необходимо найти координаты
необходимо найти координаты 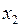 и
и 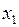 точек
точек 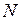 и
и 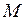 конца и начала стержня в один и тот же момент времени
конца и начала стержня в один и тот же момент времени 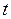 по часам в системе
по часам в системе  :
: 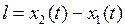 .
.
Из преобразований Лоренца следует, что
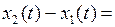
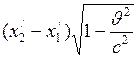 , или
, или
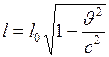 . (I.163)
. (I.163)
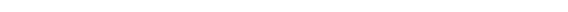
Длина тела зависит от скорости его движения. Собственная длина тела является его наибольшей длиной. Линейный размер тела, движущегося относительно инерциальной системы отсчёта, уменьшается в направлении движения в 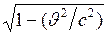 раз (лоренцево сокращение длины).
раз (лоренцево сокращение длины).
Лоренцево сокращение длины является кинематическим эффектом специальной теории относительности и не связано с действием каких-либо сил, «сдавливающих» стержень вдоль его длины.

В полном соответствии с принципом относительности эффект сокращения длины стержня является взаимным: если такой же стержень покоится в системе отсчёта  , то его длина в этой системе отсчёта равна
, то его длина в этой системе отсчёта равна 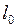 , а в системе
, а в системе 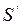 длина будет меньше в соответствии с приведённой формулой.
длина будет меньше в соответствии с приведённой формулой.
Как видно из формулы (I.163), эффект сокращения длины зависит от относительной скорости 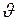 систем отсчёта и становится особенно заметным для скоростей, сравнимых со скоростью света. При
систем отсчёта и становится особенно заметным для скоростей, сравнимых со скоростью света. При 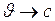 ,
, 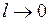 . Зависимость лоренцева сокращения от скорости показана на рисунке 45.
. Зависимость лоренцева сокращения от скорости показана на рисунке 45.
Из лоренцева сокращения следует, что никакое тело не может двигаться в пространстве со скоростью 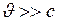 . Иначе это означало бы, что длина тела является мнимой величиной или обращается в нуль.
. Иначе это означало бы, что длина тела является мнимой величиной или обращается в нуль.
В. Замедление времени
Теперь перейдём ко второму основному измерению – измерению хода часов.
Если два события в системе  происходят в одной и той же точке не одновременно, а разделены интервалом времени
происходят в одной и той же точке не одновременно, а разделены интервалом времени 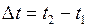 (этот промежуток времени называют собственным временем), то интервал
(этот промежуток времени называют собственным временем), то интервал 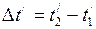 в системе
в системе 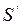 тех же событий в системе
тех же событий в системе  в соответствии с (I.161) будет определяться формулой
в соответствии с (I.161) будет определяться формулой
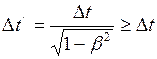 (I.164)
(I.164)
Соответственно для  получаем
получаем
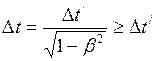 (I.165)
(I.165)
Если одна система отсчёта движется относительно другой, то временной интервал между двумя событиями в «движущейся» системе отсчёта оказывается больше, чем в «неподвижной» системе (парадокс часов).
Временной интервал между двумя событиями зависит от системы отсчёта, т.е. является относительной.
Так как при любой скорости отличной от нуля 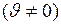
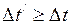 , то собственное время меньше, чем промежуток времени между этими же событиями, измеренный в любой другой системе отсчёта. Этот эффект называют релятивистским замедлением или «растяжением» времени. Замедление времени является следствием инвариантности скорости света.
, то собственное время меньше, чем промежуток времени между этими же событиями, измеренный в любой другой системе отсчёта. Этот эффект называют релятивистским замедлением или «растяжением» времени. Замедление времени является следствием инвариантности скорости света.
С эффектом замедления времени связан так называемый парадокс близнецов. Парадокс близнецов – мысленный эксперимент с двумя близнецами, движущимися относительно друг друга. Согласно эффекту релятивистского замедления времени каждый из близнецов считает (и это подтверждается его наблюдениями), что часы другого близнеца идут медленнее, чем его часы. Если один из близнецов улетит, а потом вернётся, то кто из них окажется младше?
Согласно специальной теории относительности младше окажется улетевший и вернувшийся. Возникает парадокс: «Почему, если каждый видел, что время замедляется у другого, младше становится именно улетавший?»
Попробуем дать простейшее объяснение данному парадоксу.
Близнец, который вернулся, неизбежно должен был изменить свою скорость. Поэтому его система отсчёта не является инерциальной (он должен двигаться с ускорением). А согласно СТО равноправны только инерциальные системы. Следовательно, нет ничего удивительного, что системы оказываются несимметричными.
Хотя такая ситуация и необычна, в ней нет внутреннего противоречия, а многочисленные эксперименты по релятивистскому замедлению времени подтверждают теорию относительности и дают основание утверждать, что так и будет на самом деле.
Вследствие замедления времени и сокращения длины скорость в инерциальной системе, движущейся относительно данной системы, также изменяется по величине и направлению.
С. Релятивистский закон сложения скоростей
Ещё одним важным следствием из преобразований Лоренца является изменение теоремы сложения скоростей по сравнению с классической механикой [1]
Существует два способа сложения скоростей в зависимости от того, в какой системе отсчёта определены эти скорости.
I способ . Правило параллелограмма.

Пусть тело за время  смещается из точки
смещается из точки 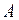 в точку
в точку 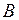 на вектор
на вектор 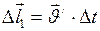 (по определению средней скорости тела). Затем, за тоже время, тело из точки
(по определению средней скорости тела). Затем, за тоже время, тело из точки 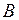 смещается в точку
смещается в точку 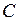 на вектор
на вектор 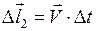 . Согласно правилу параллелограмма для смещений
. Согласно правилу параллелограмма для смещений 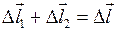 , где
, где 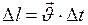 (рис.46). Заменим
(рис.46). Заменим 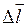 ,
, 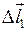 и
и 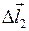 их значениями, тогда можно будет записать следующее выражение
их значениями, тогда можно будет записать следующее выражение 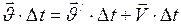 . Отсюда получаем параллелограмм скоростей
. Отсюда получаем параллелограмм скоростей
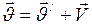 ,(I.166)
,(I.166)
который никак не связан с принципом относительности, так как все рассуждения проводились в одной и той же системе отсчёта, где измерены 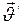 и
и 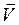 . Уравнение (I.166) представляет собой разложение вектора на составляющие.
. Уравнение (I.166) представляет собой разложение вектора на составляющие.
II способ . Правило Эйнштейна.
Совсем другая ситуация возникает, когда необходимо сделать пересчёт скоростей из одной системы отсчёта в другую.
Закон сложения скоростей в механике Ньютона противоречит постулатам СТО и заменяется в СТО новым, релятивистским законом сложения скоростей. Релятивистским называется закон сложения скоростей, вытекающий из преобразований Лоренца. Этот закон удовлетворяет постулатам СТО и предельному характеру скорости света в вакууме.

Если материальная точка или тело 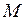 движется вдоль осей
движется вдоль осей  и
и 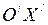 в инерциальных системах
в инерциальных системах  и
и 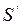 и имеет в этих системах скорости, равные соответственно
и имеет в этих системах скорости, равные соответственно 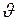 и
и 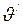 , то
, то
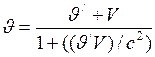 , (I.167)
, (I.167)
где 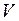 - скорость движения системы
- скорость движения системы 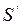 относительно оси
относительно оси  системы
системы  (рис.47).
(рис.47).
Используя обратные преобразования Лоренца для перехода от параметров системы 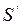 и
и  , мы можем получить формулу такой же структуры, в которой
, мы можем получить формулу такой же структуры, в которой 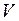 заменяется на
заменяется на 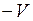 :
:
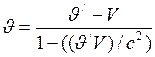 . (I.168)
. (I.168)
Что полностью согласуется с принципом эквивалентности всех инерциальных систем отсчёта.
Формула (I.167), представляет собой закон сложения скоростей в специальной теории относительности.
Пусть в (I.168) 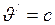 , отсюда следует, что
, отсюда следует, что 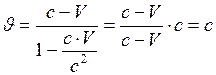 , т.е.
, т.е. 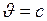 вне зависимости от скорости системы отсчёта.
вне зависимости от скорости системы отсчёта.
При 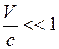 и
и 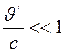 и произвольной скорости
и произвольной скорости 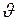 релятивистский закон сложения скоростей переходит в закон сложения скоростей механики Ньютона:
релятивистский закон сложения скоростей переходит в закон сложения скоростей механики Ньютона:
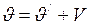 . (I.169)
. (I.169)
Из релятивистского закона сложения скоростей следует, что сумма двух скоростей, меньших или равных 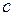 , есть скорость, не большая
, есть скорость, не большая 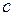 . В частности, если
. В частности, если 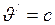 , то
, то 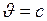 при любой скорости
при любой скорости 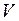 . При
. При 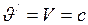 получается, что и
получается, что и 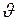 равно
равно 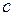 . Это подтверждает тот факт, что, в теории относительности при сложении любых скоростей результат не может превысить скорости света в вакууме
. Это подтверждает тот факт, что, в теории относительности при сложении любых скоростей результат не может превысить скорости света в вакууме 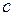 .
.
Следует заметить, что именно скорость света в вакууме есть предельная скорость, которую нельзя превысить.
Дата добавления: 2016-09-06; просмотров: 5685;











