Аморфные и кристаллические тела. Анизотропия кристаллов. Классификация кристаллов по типу связей. Дефекты в кристаллах. Жидкие кристаллы.

В природе встречаются две группы твердых веществ существенно отличающиеся своими свойствами: кристаллические и аморфные. В физике к твердым телам относятся только те, которые имеют кристаллическое строение. Металлы, соли, лед, песок, горные породы, многие синтетические материалы являются кристаллическими телами.

Основная особенность кристаллического вещества - регулярное, правильное расположение частичек, которое бесконечно повторяется в пространстве. Силы, действующие между частичками, удерживают их в данном положении, создавая пространственные кристаллические решетки. В узлах этих решеток могут находиться атомы, ионы, молекулы, которые беспрерывно колеблются возле положения равновесия.

Одна из основных особенностей кристаллических тел - анизотропия, т.е. различие физических свойств в разных направлениях. Кристаллы легко раскалываются в одних направлениях (плоскости спайности) и тяжелее в других. Упругость кристаллов разная вдоль разных осей, разная теплопроводность, скорость распространения света в разных направления различная и т.д. У многих кристаллов анизотропия резко не проявляется. Такие кристаллы состоят из множества маленьких кристаллов ориентированных хаотично. Такие тела называются поликристаллическими, в отличие от монокристаллов – твердых тел, кристаллическая решетка которых единая по всему объему. При правильном расположении атомов, они размещаются вдоль разных направлений с различной плотностью. Этим и обусловлена анизотропия свойств кристаллов. (рис.1):

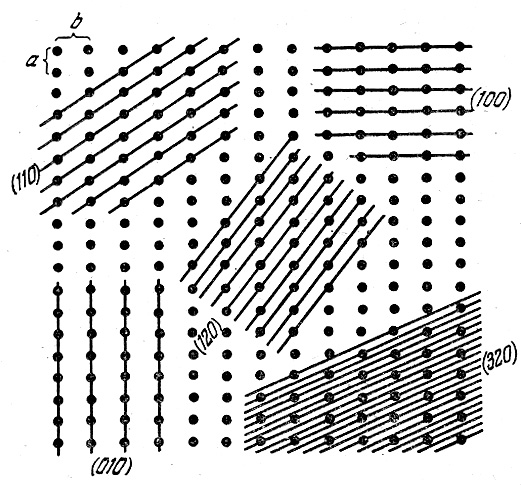
Рис.1. Плотность размещения атомов в различных направлениях

В отличие от кристаллических тел в аморфных телах, как и в жидкостях, наблюдается ближний порядок в размещении частиц. Аморфные тела (стекло, смола, пластмассы и т.д.) – это сильно переохлажденные жидкости. С понижением температуры их вязкость возрастает настолько, что они теряют способность течь. При этом у них сохраняется молекулярная структура характерная для жидкостей. Аморфные тела изотропные, т.е. их физические свойства одинаковые по всем направлениям.

Кристаллические тела имеют определенную температуру плавления. Аморфные тела при нагревании постепенно размягчаются, вязкость их уменьшается, и они начинают вести себя как маловязкие жидкости. Некоторые вещества могут существовать в кристаллической и аморфной формах (кварц, сера, сахар и т.д.). Аморфная форма кристаллического тела неустойчивая. С течением времени такие тела самопроизвольно переходят в кристаллическую форму (засахаривание варенья, меда).

Кристаллы каждого вещества обладают своей характерной формой. Для данного вещества углы между соответствующими гранями, ребрами являются строго постоянными.

Структуру любого кристалла можно однозначно определить с помощью элементарной ячейки.

Элементарная ячейка это наименьший элемент кристалла, многократным перемещением которого выстраивается трехмерная пространственная решетка.

Выбор элементарной ячейки для данной кристаллической структуры можно осуществить многими способами (рис.2,б):

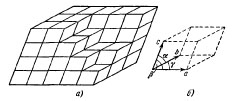
Рис.2. Элементарная ячейка – б некоторого кристалла – а

Элементарная ячейка представляет собой параллелепипед, который построен на векторах a, b, c, модули которых равны периоду повторяемости, например, расстоянию между атомами решетки. Направление ребер характеризуется углами α, β, γ между ребрами ячейки. Величины a, b, c, α, β, γ однозначно определяют элементарную ячейку и называются ее параметрами.

Если элементарную ячейку перемещать в пространстве вдоль направлений a, b, c параллельно самой себе на расстояния a, b, c, то будет создана бесконечная, периодическая, пространственная структура, которая называется пространственной решеткой (рис.2,а). Такие перемещения называются трансляциями. Место расположения частичек (молекулы, атомы) – вершины параллелепипеда, называются узлами пространственной решетки. Положение любого узла решетки определяется уравнением:

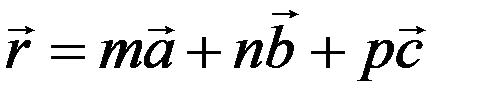(1)

где m,n,p – целые числа, которые определяют номер узла по соответствующей оси (a, b, c). Эти числа называются символами узла.

Пространственную решетку можно также описать узловыми или кристаллическими плоскостями. Кристаллическая плоскость это плоскость, в которой находится бесконечное множество узлов (молекул, атомов) решетки. Каждую кристаллическую плоскость можно описать уравнением:

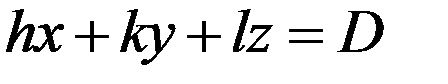(2)

где h,k,l – целые числа, D – любое число. Числа h,k,l однозначно определяют направление плоскости в пространстве и называются индексами Миллера.

Рассмотрим элементарную ячейку кубической решетки:

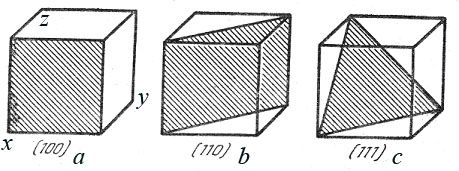
Рис.3. Кристаллические плоскости

Штрихованная грань (рис.3,a) описывается уравнением:

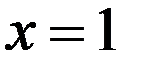
Или уравнением (2):

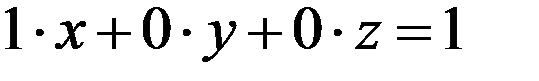
Следовательно:

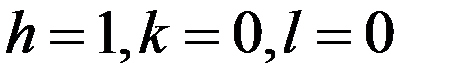
Для этой плоскости индексы Миллера – (100).

Для классификации кристаллов используются решетки Браве. Решетка Браве это параллелепипед, построенный путем переноса какого-нибудь узла решетки по трем направлениям (координатным осям). Простейшая, примитивная ячейка содержит 8 частиц в восьми вершинах параллелепипеда. Ячейки отличаются одна от другой: ребра a, b, c равные или нет, углы α, β, γ прямые или непрямые. При такой классификации возможны семь систем кристаллических решеток. Эти типы решеток простые. Например, кубическая (рис.4, 1):

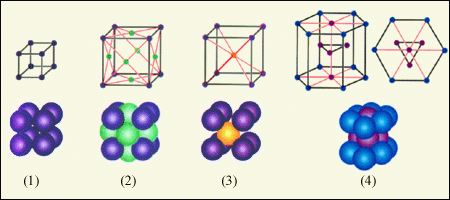
Рис.4. Кристаллические решетки: 1 – простая кубическая решетка; 2 – гранецентрированная кубическая решетка; 3 – объемноцентрированная кубическая решетка; 4 – гексагональная решетка.

Для простой кубической решетки:

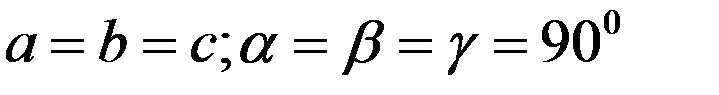
Существуют и сложные кристаллические решетки, которые содержат узлы (атомы, молекулы) внутри объема параллелепипеда и на его гранях (рис.4, 2,3,4). Сложных кристаллических решеток существует также семь. Следовательно, всего существует 14 различных типов решеток Браве (рис.5).

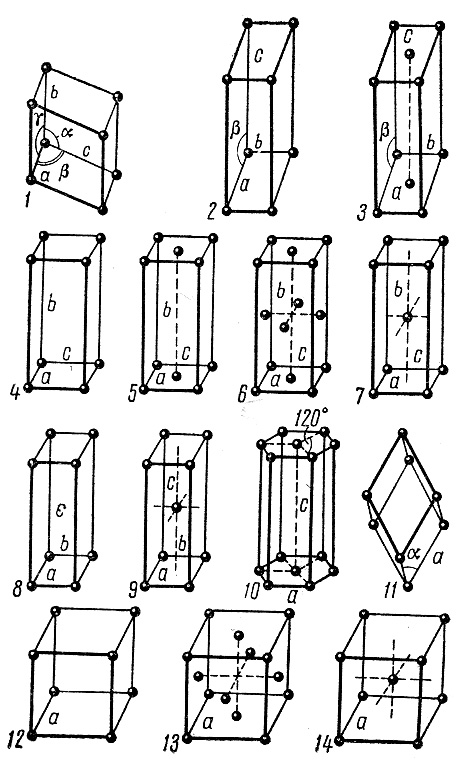
Рис.5. Решетки Браве

Кристаллические решетки могут складываться из нескольких решеток, как бы вставленных одна в другую. Кристаллическая решетка NaCl (поваренная соль) складывается из двух кубических гранецентрированных решеток, которые смещены друг относительно друга на половину ребра куба (рис.6):

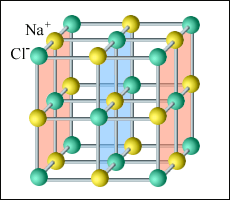
Рис.6. Кристаллическая решетка поваренной соли

Частицы в кристалле расположены таким образом, чтобы энергия взаимодействия между ними была минимальной.

Энергией связи частицы в кристалле называется энергия необходимая для удаления частицы из кристалла.

В зависимости от того, какие частицы находятся в узлах кристаллической решетки и от характера сил взаимодействия между ними возможны следующие типы кристаллов:

Кристаллы с ионной связью или ионные кристаллы. В узлах решетки находятся ионы разных знаков. Ионы размещаются так, что силы притяжения между ионами разных знаков уравновешиваются силами отталкивания между ионами одинаковых знаков. Связь осуществляется кулоновскими силами и называется гетерополярной. Энергия связи 10⁵ – 10⁶ Дж/моль. Типичные ионные кристаллы NaCl, CsCl, CaF₂. Энергия связи большая, поэтому кристаллы прочные, температуры плавления высокие.

Кристаллы с ковалентной связью – атомные кристаллы. В узлах решетки находятся нейтральные атомы. Между ними устанавливается ковалентная (гомеополярная) связь, при которой валентные электроны, по одному от каждого атома, двигаются по одной орбите вокруг двух атомов. В зависимости от валентности атома связь может осуществляться одной, двумя, тремя и четырьмя парами электронов. Энергия связи 10⁵ – 10⁶ Дж/моль. Такая связь очень сильная. Об этом свидетельствует высокая твердость и температура плавления таких кристаллов как алмаз, кремний.

Кристаллы с металлической связью – металлические кристаллы. В узлах решетки находятся положительные ионы, между которыми двигаются свободные (валентные) электроны, которые и обеспечивают связь между ионами. Энергия связи 10⁴–10⁵ Дж/моль. Температуры плавления высокие, кристаллы механически прочные.

Структура металлического кристалла

Кристаллы с ван-дер-ваальсовской связью – молекулярные кристаллы. В узлах таких кристаллов находятся ориентированные определенным образом молекулы. Связь осуществляется ван-дер-ваальсовскими молекулярными силами. Энергия связи 10³ – 10⁴ Дж/моль. Температуры плавления низкие, механическая прочность маленькая (кристаллы затвердевших инертных газов).

Кристаллы с водородной связью. Они возникают благодаря электрическому взаимодействию атома водорода с другими атомами. Энергия связи ~ 10⁴ Дж/моль. Представители: кристаллы льда, сегнетоэлектрики триглицинсульфат (TGS), КДР (KH₂PO₄).

В некоторых кристаллах осуществляется несколько видов связей. Графит имеет слоистую структуру. Три атома в слое связаны сильной ковалентной связью, а слои между собой слабой молекулярной связью. Поэтому слои графита легко скользят относительно друг друга (карандаш) (рис.7):

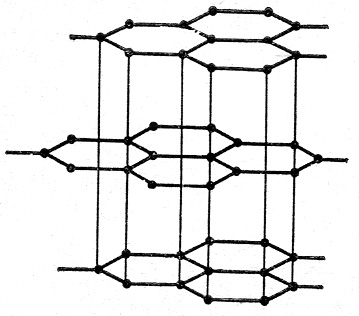
Рис.7. Решетка графита

Идеально правильная структура кристалла наблюдается в относительно небольших объемах. Реальные кристаллы имеют различные нарушения регулярной структуры – дефекты. Наличие дефектов сильно влияет на физические свойства кристаллов. Различают точечные дефекты и дислокации.

Точечные дефекты: между регулярно размещенных узлов может находиться незанятый узел – дефект по Шоттки или вакансия. Если частица внедряется между узлами, наблюдается дефект по Френкелю (рис.8):

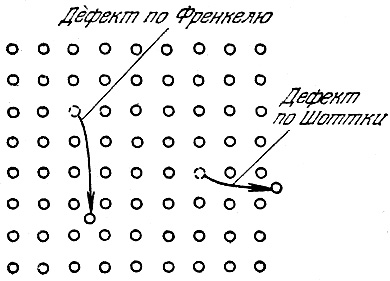
Рис.8. Дефекты в кристаллах

Иногда узел может быть занят частицей другого вида - примесь внедрения. Во всех этих случаях нарушается геометрия решетки, возникают механические напряжения (рис.9):

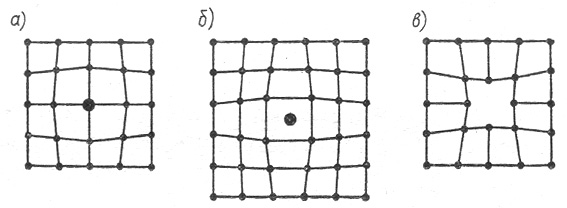
Рис.9. Искажения кристаллической решетки

Дислокации. Различают линейные и винтовые дислокации. Линейная дислокация наблюдается в случае отсутствия части кристаллической плоскости (рис.10):

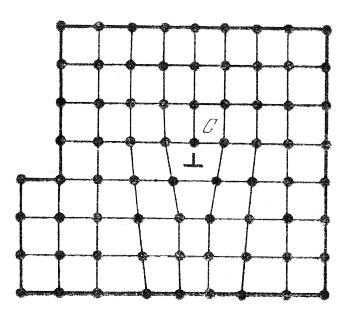
Рис.10. Линейная дислокация

Соседние кристаллические плоскости сдвигаются, заполняя место отсутствующей плоскости.

Винтовая дислокация появляется из-за сдвига одной части кристалла относительно другой (рис.11):

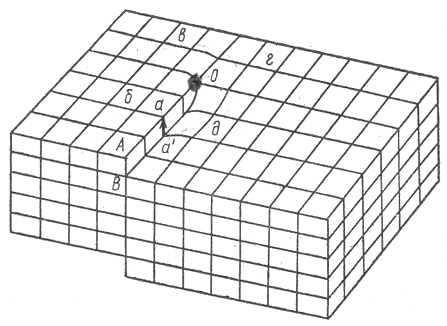
Рис.11. Винтовая дислокация

В результате сдвига, при обходе плоскости вокруг некоторой точки О получается винтовая линия.

Важнейшим свойством дислокаций является их легкая подвижность. Уже при слабых механических воздействиях дислокации начинают перемещаться. При этом уменьшается механическая прочность кристаллов. Дислокации можно закрепить введением примесей, которые препятствуют движению дислокаций. Это сильно увеличивает прочность кристаллов. В металлах таких примесей достаточно ~ 0,01% - легирование металлов. Другой путь увеличения прочности кристаллов – выращивание бездефектных кристаллов. Прочность таких кристаллов (монокристаллические усы) достигает теоретических значений.

Многие вещества могут находиться в своеобразном состоянии, которое называется жидкокристаллическим. По своим свойствам эти вещества приближаются к жидкостям: они текучи, могут существовать в виде капель. Однако в этих веществах, как и в кристаллах, наблюдается пространственная анизотропия, проявляющаяся в оптических и других свойствах.

В зависимости от ориентации молекул различают нематические, смектические и холестерические жидкие кристаллы. Способность веществ образовывать жидкие кристаллы, обусловлена особенностями строения их молекул. Обычно это удлиненные или дискообразные молекулы.

В нематических жидких кристаллах эти молекулы ориентируются так, что их оси параллельны друг другу. В микроскоп наблюдаются нитеобразные образования (рис.12):

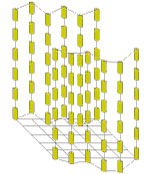
Рис.12. Структура нематиков

Смектические жидкие кристаллы характеризуются слоистым расположением молекул, причем продольные оси молекул ориентированы перпендикулярно к поверхности слоев.

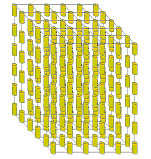
Рис.13. Структура смектиков

В холестерических жидких кристаллах молекулы ориентированы так, что их оси при переходе от слоя к слою описывают винтовую линию.

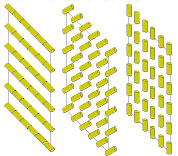
Рис.14. Структура холестериков

Жидкие кристаллы очень чувствительны к изменению внешних условий. Их свойства резко изменяются при изменении температуры, электрических полей, под действием света. На этих эффектах и основано их практическое применение (ЖК – индикаторы, LCD, TFT – дисплеи и т.д.).

Лекция 22

Тепловые свойства кристаллов. Тепловое расширение. Теплоемкость кристаллов. Закон Дюлонга и Пти. Трудности классической физики в объяснении температурной зависимости теплоемкости твердых тел.

Тепловое движение частичек в кристаллах существенно отличается от теплового движения молекул в газах и жидкостях. Частички в кристаллах совершают колебания возле положений равновесия – узлов кристаллической решетки. При отклонении частички от положения равновесия возникает сила, которая стремиться вернуть ее в положение равновесия. При малых отклонениях эти силы квазиупругие и колебания частичек гармонические. При комнатных температурах амплитуда колебаний ~ 0,1 межатомного расстояния, это значит 1 – 2 нм.

Тепловые колебания частичек не имеют определенной ориентации. Это сложные колебания, которые определяются связями с соседними частичками. Энергия колебательного движения частичек зависит от температуры и определяет внутреннюю энергию кристалла. При понижении температуры внутренняя энергия уменьшается. Однако при T → 0 внутренняя энергия стремится не к нулю, а, согласно квантовой теории, к некоторому значению U₀, которое называется нулевой энергией. Нулевая энергия обычно значительно меньше энергии взаимодействия частичек.

При нагревании твердые тела расширяются. При увеличении температуры увеличивается амплитуда колебаний и энергия частичек. Однако увеличение амплитуды колебаний не может объяснить тепловое расширение твердых тел, потому что с ростом амплитуды положение равновесия частичек изменяться не должно.

Тепловое расширение вызывается увеличением энергии колеблющихся частичек. Колебания становятся ангармоническим (не гармоническими).

Рассмотрим кривую зависимости потенциальной энергии частичек от расстояния между ними (рис.1):

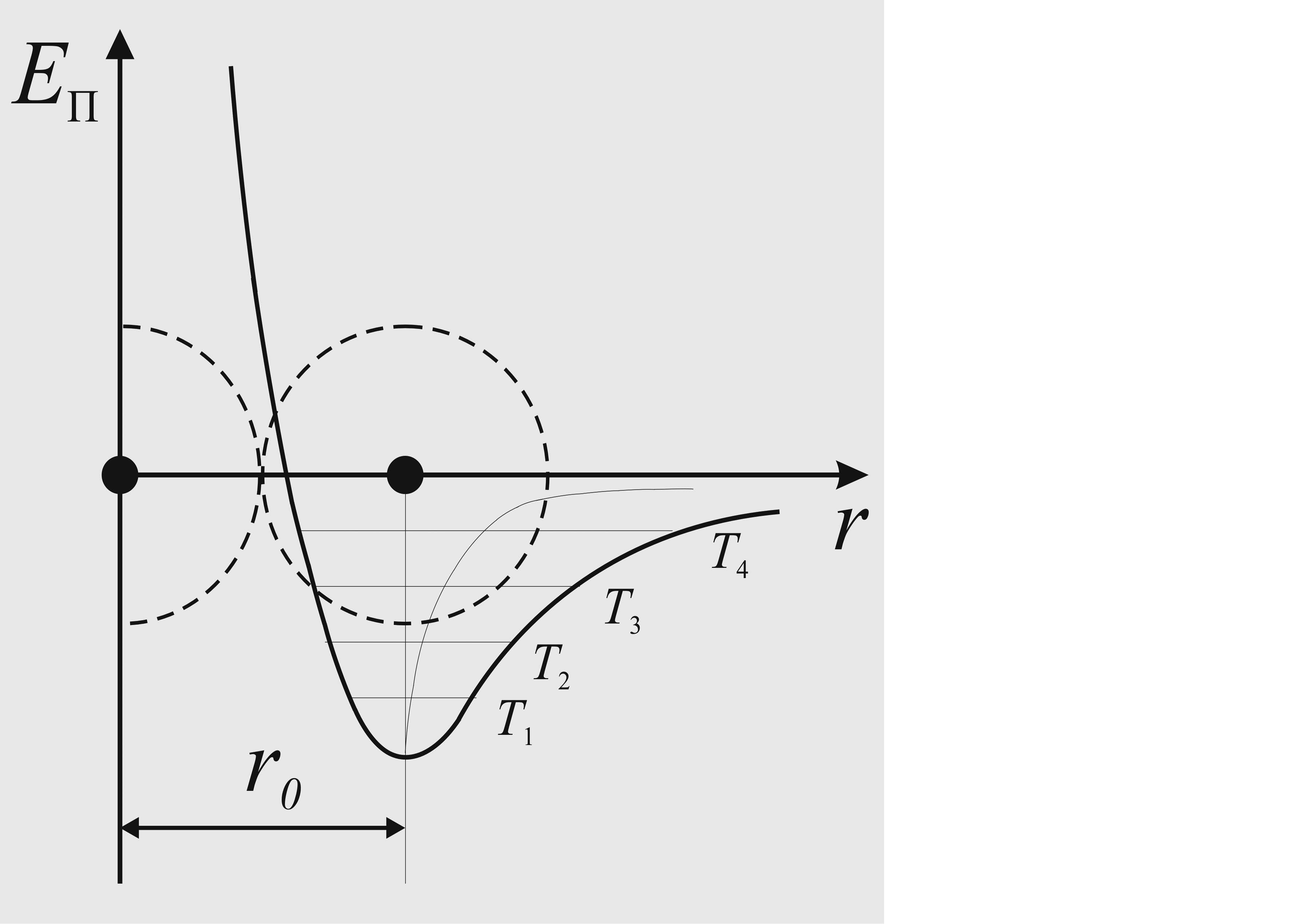
Рис.1. Тепловое расширение кристаллов: T₄>T₃>T₂>T₁

Пусть горизонтальные прямые показывают уровни энергии атома в кристаллической решетке при разных температурах (T₁, T₂ и т.д.). Точки пересечения прямых с кривой энергии определяют крайние положения атома, которые он занимает при колебаниях. Середина прямой определяет положение равновесия атома при данной температуре.

При повышении температуры атом переходит на более высокие энергетические уровни.

Из-за разной зависимости сил притяжения и отталкивания от расстояния между атомами, кривая потенциальной энергии асимметрична в верхней части.

Вследствие асимметричности кривой зависимости E_п(r), центры прямых при повышении температуры смещаются вправо, что означает смещение положения равновесия атома, т.е. увеличение межатомного расстояния.

Следовательно, причиной теплового расширения твердых тел при нагревании является не увеличение амплитуды колебания атомов, а увеличение межатомных расстояний, которые характеризуют новое положение равновесия.

Пусть при температуре T₁ длина тела l, а при температуре T₂ - l′. Опыты показали:

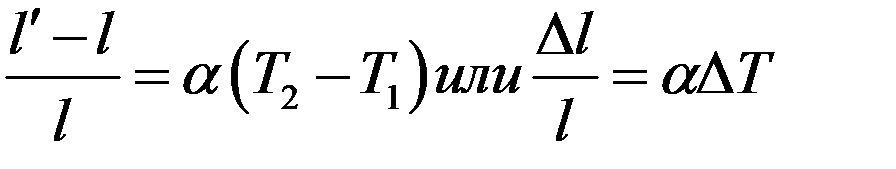(1)

где коэффициент пропорциональности α – коэффициент линейного расширения, ∆l/l – относительное удлинение.

Из (1):

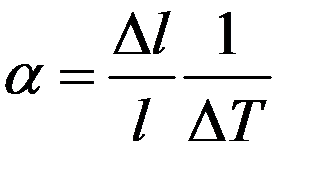(2)

Коэффициент линейного расширения численно равен относительному удлинению при повышении температуры на 1K.

Для большинства твердых тел α ≈ 10^-5 – 10^-6 K^-1. Величина α несколько уменьшается с понижением температуры.

Из-за анизотропии кристаллов, коэффициент линейного расширения разный для разных направлений. Поэтому, если в кристалле провести произвольную прямую, то при повышении температуры она не будет оставаться прямой.

Однако в любом кристалле существуют такие направления, вдоль которых прямая будет оставаться прямой и при тепловом расширении кристалла. Такие направления называются кристаллографическими осями.

Значения коэффициента линейного расширения вдоль этих осей называются главными. В зависимости от типа решетки, кристаллы могут иметь одну (одноосные), две (двухосные), три (трехосные) кристаллографические оси и, соответственно, один, два, три главных коэффициента линейного расширения.

При нагревании возрастает, и объем твердого тела. Установлено, что относительное изменение объема тела пропорционально изменению температуры:

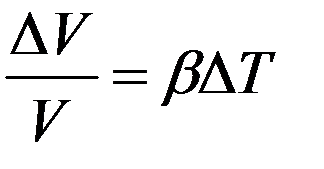(3)

где ∆V/V – относительное изменение объема тела при изменении температуры на ∆T. Коэффициент пропорциональности β называется коэффициентом объемного расширения:

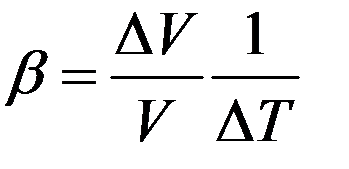(4)

Коэффициент объемного расширения численно равен относительному изменению объема при изменении температуры на 1K.

Если α₁, α₂, α₃ – главные коэффициенты линейного расширения кристалла, то коэффициент его объемного расширения определяется выражением:

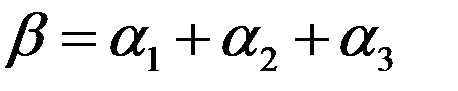(5)

Для кристаллов с кубической решеткой и для всех изотропных тел:

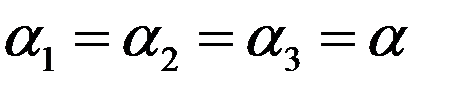(6)

Для этих тел:

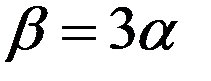(7)

Если при нагревании твердое тело не имеет возможности свободно расширяться, то возникают очень большие напряжения, которые надо учитывать на практике.

При нагревании твердого тела теплота идет на увеличение энергии колебаний атомов. Энергия колебательного движения складывается из кинетической и потенциальной энергии. Каждое колебание можно разложить на три составляющих по осям координат. Поэтому каждая частица обладает тремя колебательными степенями свободы i_к = 3.

При гармонических колебаниях кинетическая энергия колебательного движения равна потенциальной. Согласно закону равномерного распределения энергии по степеням свободы на каждую колебательную степень свободы приходится 1/2kT в виде кинетической энергии и 1/2kT в виде потенциальной. Следовательно, полная энергия колеблющейся частицы будет равна:

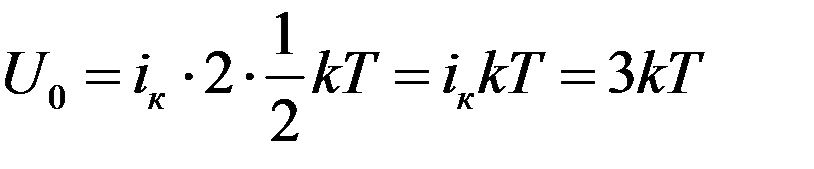(8)

Внутренняя энергия 1 моля твердого тела:

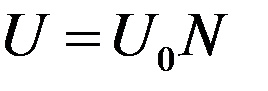(9)

где N – число частиц в одном моле твердого тела.

Для химически простых веществ число частиц в 1 моле равно числу Авогадро N = N_a. Тогда из (8) и (9):

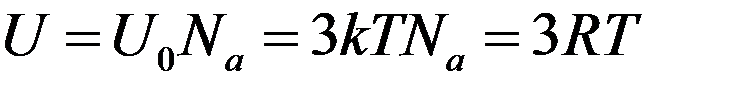(10)

Коэффициент объемного расширения твердых тел очень мал, поэтому C_p ≈ C_V = C. Следовательно, вся теплота, подведенная к твердому телу, идет на увеличение его внутренней энергии. Тогда молярная теплоемкость твердого тела:

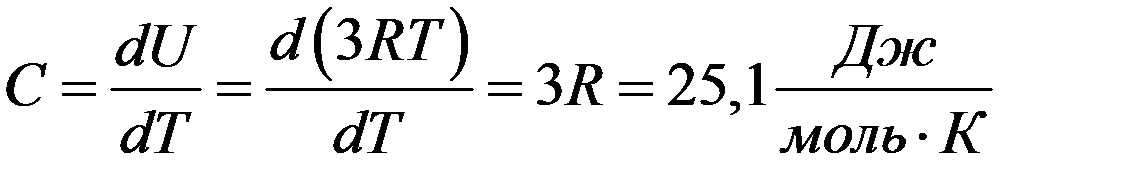(11)

Согласно (11) молярная теплоемкость химически простых твердых тел равна 3R и не зависит от температуры. Это закон Дюлонга и Пти (1818г.). Закон Дюлонга и Пти хорошо выполняется для многих веществ при комнатных температурах.

При определении молярной теплоемкости химически сложных веществ необходимо учитывать общее число частиц в 1 моле данного вещества. У химически сложных веществ общее число частиц в 1 моле равно числу Авогадро умноженному на число атомов, из которых складывается молекула данного вещества. Например, KCl – в одном моле N_a атомов калия и N_a атомов хлора – всего 2N_a частиц. Молярная теплоемкость такого кристалла 2*3R = 6R. В случае трехатомных молекул молярная теплоемкость 9R, четырехатомных - 12R.

Эти рассуждения совпадают с эмпирически установленным законом Неймана-Коппа:

Молярная теплоемкость твердых соединений равна сумме атомных теплоемкостей элементов, которые входят в это соединение:

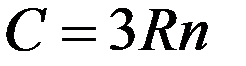(12)

где n – число атомов, входящих в молекулу данного соединения.

Этот закон, также как и закон Дюлонга и Пти выполняется при довольно высоких температурах, при которых колебания частиц можно считать независимыми.

Некоторые вещества не подчиняются закону Дюлонга и Пти. Молярная теплоемкость алмаза при комнатных температурах, много меньше 3R, и только при температурах больших, чем 1000 ^оC она приближается к значению 3R.

Это не единственное отклонение от закона Дюлонга и Пти. При низких температурах теплоемкость кристаллических веществ быстро уменьшается и стремится к нулю при абсолютном нуле температуры (рис.2).

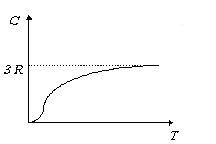
Рис.2. Зависимость теплоемкости от температуры

Вблизи абсолютного нуля теплоемкость всех кристаллов пропорциональна T³, и только при достаточно высокой температуре, характерной для каждого вещества, начинают выполняться законы Дюлонга и Пти (11) и Неймана-Коппа (12).

Эти законы являются следствием закона о равномерном распределении энергии по степеням свободы. Тот факт, что твердые тела не подчиняются этим законам, свидетельствует о том, что закон о равномерном распределении энергии по степеням свободы является приблизительным, и не применим при низких температурах.

Точная, квантовая теория теплоемкости кристаллов была создана Эйнштейном и Дебаем. Квантовая теория теплоемкости учитывает:

1. Квантование энергии колебательного движения – энергия колебательного движения может принимать только некоторые, дискретные значения;

2. Колебания частиц в кристаллической решетке не являются независимыми.

Из теории Дебая следует, что при температурах близких к абсолютному нулю, внутренняя энергия твердого тела пропорциональна четвертой степени температуры:

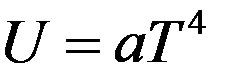(13)

где a – постоянная, зависящая от частоты колебаний частиц.

Следовательно, теплоемкость кристаллов:

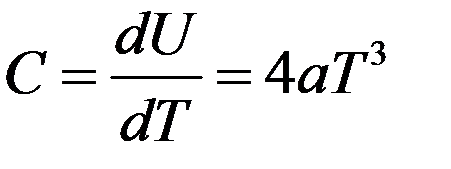(14)

(14) – закон кубов Дебая. Из теории Дебая следует, что, начиная с некоторой температуры разной для разных веществ (характеристическая температура Дебая) теплоемкость начинает быстро уменьшаться с понижением температуры.

Температура Дебая считается границей между низкими и высокими температурами (и не только для теплоемкости). Температура Дебая для серебра – 210 ^oC, алюминия – 400 ^oC, алмаза – 2000 ^oC.

Для кристаллов, не подчиняющихся закону Дюлонга и Пти при комнатных температурах (алмаз, бор, кремний), характеристические температуры больше 1000 ^oC, и поэтому комнатные температуры являются для них низкими.

Как показали опыты, для некоторых веществ теплоемкость пропорциональна T², а для некоторых ~ T. Это связано с особенностями строения кристаллической решетки. Если частицы связаны с соседними частицами одинаково сильно во всех трех направлениях – выполняется закон кубов Дебая. Если вещество имеет слоистую структуру (графит, слюда), то связь частиц в двух направлениях (в одной плоскости) сильнее, чем в третьем направлении (между слоями). Для этих веществ теплоемкость ~ T². Если вещество складывается из частиц с цепочной связью и цепи связаны между собой слабо, то теплоемкость ~ T (HF, BiO₃, плавленый кварц).

Лекция 23