I.3.3 МЕХАНИЧЕСКАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ

Энергией называется скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие.

Механическая энергия характеризует движение и взаимодействие тел и является функцией скоростей и взаимного расположения тел. Она равна сумме кинетической и потенциальной энергий.

Кинетическая энергия материальной точки или тела является мерой их механического движения, зависящей от скоростей их движения в данной инерциальной системе отсчёта.

Кинетическая энергия материальной точки 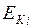с массой 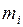, движущейся в данной инерциальной системе отсчёта со скоростью 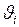, или имеющей импульс 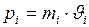, равна

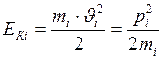. (I.78)

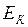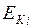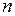Кинетическая энергия системы складывается из кинетических энергий всех материальных точек, из которых состоит система: 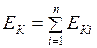. При поступательном движении тела его кинетическая энергия равна половине произведения массы 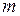тела на квадрат скорости 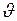любой из его точек, или квадрату импульса 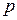тела, делённому на удвоенную массу тела:

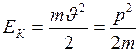. (I.79)

Значения кинетической энергии материальной точки или тела зависят от выбора системы отсчёта, но не могут быть отрицательными ( ).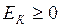

Теорема о кинетической энергии: изменение кинетической энергии 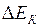тела при его переходе из одного положения в другое равно работе 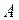всех сил, действующих на тело:

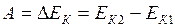, (I.80)

где 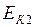- кинетическая энергия тела в конечном положении;

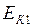- кинетическая энергия в начальном положении.

Работа любых сил является мерой изменения кинетической энергии тела или материальной точки. Действие сил, работа которых на данном участке траектории положительна, приводит к увеличению кинетической энергии тела. Действие сил, работа которых отрицательна, приводит к уменьшению кинетической энергии тела.

Потенциальной энергией 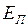называется часть механической энергии, зависящая от конфигурации системы, т.е. от взаимного расположения её частей и их положения во внешнем силовом поле. Потенциальная энергия зависит от относительного расположения взаимодействующих материальных точек, тел (или их частей) и относится ко всей совокупности (системе) взаимодействующих объектов.

Так как во всех практических задачах интерес представляет разность значений потенциальной энергии, нуль отсчёта потенциальной энергии выбирают произвольно. В связи с этим потенциальная энергия может быть положительной, отрицательной или равной нулю.

Мерой изменения потенциальной энергии системы при её переходе из одного состояния в другое является работа потенциальных сил, осуществляющих взаимодействие между элементами системы. При этом работа 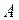потенциальных сил равна изменению 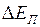потенциальной энергии системы при её переходе из начального состояния в конечное, взятое с обратным знаком:

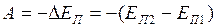, (I.81)

где 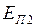- потенциальная энергия системы в конечном состоянии;

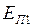- потенциальная энергия системы в начальном состоянии.

А. Потенциальная энергия тела, на которое действует сила тяжести – физическая величина, равная произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли,

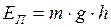. (I.82)

Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:

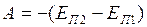(I.83)

Значение потенциальной энергии тела, поднятого над Землёй, зависит от выбора нулевого уровня, т. е. высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.

При таком выборе нулевого уровня потенциальная энергия тела, находящегося на некоторой высоте над поверхностью Земли, будет определяться формулой (I.83). Данная формула показывает, что потенциальная энергия тела, на которое действует сила тяжести, равна работе, совершаемой силой тяжести при перемещении тела на нулевой уровень.

Б. Потенциальная энергия упруго деформированного тела – физическая величина, равная половине произведения жёсткости тела на квадрат его деформации,

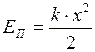. (I.84)

Потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю:

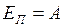. (I.85)

Работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятому, с противоположным знаком:

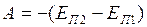. (I.86)

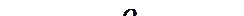Взаимные превращения кинетической и потенциальной энергии.Рассмотрим это на примере. Пусть тело массой 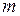падает из точки 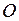(рис.30) и при падении проходит последовательно точк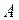и и 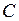на высоте 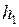и 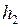: обозначив скорости тел в точках 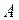и 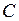соответственно 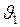и 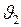, запишем уравнение изменения кинетической энергии движения из точки 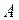в точку 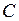(на пути )

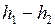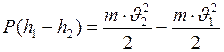, отсюда

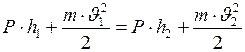. (I.87)

где 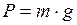- вес тела.

Это значит, что для любых точек на пути свободного падения тела сумма потенциальной и кинетической энергии есть величина постоянная.

В частном случае, если точка 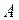есть начальная точка падения, то 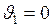, кинетическая энергия в точке 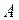- минимальная (равна нулю), а потенциальная – максимальная. Наоборот, в точке 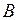при 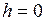, потенциальная энергия будет минимальной, а кинетическая – максимальной и скорость в этот момент принимает наибольшее значение 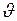. Перепишем, с учётом выше изложенного, формулу (I.87) в виде: 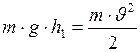. Выразим из последнего равенства, скорость движения тела: .

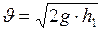Итак, при падении происходит превращение потенциальной энергии в кинетическую; при подъёме – обратно, кинетическая энергия преобразуется в потенциальную.

Следует отметить, что уравнение (I.87) применимо для всех случаев движения тел под действием силы тяжести. Его можно представить в наиболее общем виде:

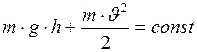. (I.88)

Уравнение (I.88) является частным случаем закона сохранения механической энергии: в изолированной системе – падающее тело – Земля – сумма потенциальной и кинетической энергии есть величина постоянная.

Если в формуле (I.88) произведение 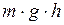, обозначить через 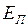, а отношение 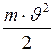, через 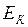, то её можно будет представить в виде:

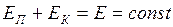, (I.89)

где 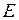- полная механическая энергия, т.е. сумма энергии механического движения 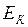и взаимодействия .

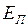Формула (I.89) представляет собой закон сохранения механической энергии: полная механическая энергия консервативной системы сохраняется постоянной в процессе движения системы.

Закон сохранения механической энергии связан с однородностью времени, т.е. инвариантностью физических законов относительно выбора начала отсчёта времени. Например, при свободном падении тела в поле сил тяжести его скорость и пройденный путь зависят лишь от начальной скорости и продолжительности свободного падения тела и не зависят от того, когда тело начало падать.

Существует ещё один вид систем – диссипативные системы, в которых механическая энергия постепенно уменьшается за счёт преобразования в другие (немеханические) формы энергии. Этот процесс получил название диссипации (или рассеяния) энергии.