I.4.3 РАБОТА. МОЩНОСТЬ. ЭНЕРГИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Работа 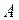 при вращательном движении вокруг данной оси равна произведению момента силы
при вращательном движении вокруг данной оси равна произведению момента силы 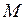 на угловое перемещение
на угловое перемещение 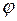 :
:
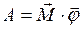 . (I.117)
. (I.117)
Формула (I.117) справедлива для случая постоянного момента силы. При изменении момента по линейному закону следует воспользоваться средним значением.
Если момент силы зависит от угла поворота, т.е. 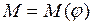 , то работа вычисляется по формуле:
, то работа вычисляется по формуле: 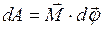 .
.
Следовательно, 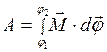 . (I.118)
. (I.118)
Мгновенная мощность (мощность) 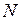 равна произведению мгновенного момента силы
равна произведению мгновенного момента силы 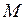 на мгновенную угловую скорость
на мгновенную угловую скорость 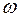 :
:
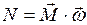 . (I.119)
. (I.119)
Эта формула справедлива также и в том случае, когда 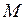 или
или 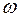 остаются постоянными; тогда мощность также постоянна.
остаются постоянными; тогда мощность также постоянна.
Вращающееся вокруг оси тело обладает кинетической энергией, т.к. все элементы его массы двигаются с определённой скоростью. Эта энергия называется энергией вращения 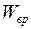 .
.
Если точка с массой 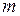 (элемент тела) движется по окружности на расстоянии
(элемент тела) движется по окружности на расстоянии 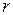 от оси, то выражение её кинетической энергии преобразовывается так:
от оси, то выражение её кинетической энергии преобразовывается так:
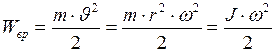 , (I.120)
, (I.120)
где 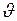 - линейная скорость точки;
- линейная скорость точки; 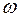 - угловая скорость точки;
- угловая скорость точки; 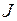 - момент инерции.
- момент инерции.
Полная энергия тела равна сумме энергий отдельных элементов тела.
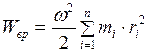 . (I.121)
. (I.121)
Или формулу (I.121) можно представить в виде:
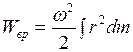 . (I.122)
. (I.122)
Обратим внимание на формулу (I.120). Сравнивая между собой кинетическую энергию вращающегося тела с энергией поступательного движения тела, мы видим, что роль массы играет момент инерции, а вместо линейной скорости стоит угловая скорость.
Итак, кинетическая энергия вращающегося тела численно равна половине произведения момента инерции его на квадрат угловой скорости.
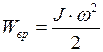 . (I.123)
. (I.123)
Следовательно, изменение скорости вращения от 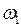 до
до 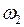 влечёт за собой изменение энергии вращения тела. Количественно изменение выражается формулой:
влечёт за собой изменение энергии вращения тела. Количественно изменение выражается формулой:
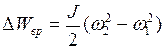 . (I.124)
. (I.124)
Сопоставление уравнений динамики поступательного движения с уравнениями вращательного движения дано в таблице 3.
Таблица 3
| движение | |
| поступательное | вращательное |
| Основной закон динамикиматериальной точки (второй закон Ньютона) | Основной закон динамики твёрдого тела, вращающегося вокруг неподвижной оси |
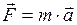 или
или 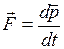
| 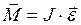
|
| Основной закон динамики твёрдого тела, вращающегося вокруг неподвижной точки | |
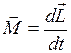
| |
| Импульс тела | Момент импульса тела |
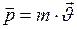
| 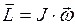
|
| Закон сохранения импульса тела | Закон сохранения момента импульса тела |
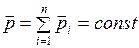
| 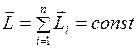
|
| Работа | |
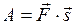
| 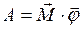
|
| Мощность | |
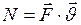 или или 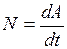
| 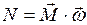 или или 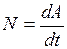
|
| Энергия | |
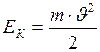
| 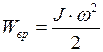
|
Дата добавления: 2016-09-06; просмотров: 11172;











