Основное уравнение газодинамики. Адиабатное течение газов. Критическая скорость.

При исследовании движений с большими скоростями, нельзя не обращать внимания на сжимаемость газов. В этих случаях необходимо применять наряду с законами аэродинамики законы термодинамики. Научная дисциплина, которая возникла на основе уточнения и развития аэродинамики с использованием законов термодинамики, называется газодинамикой.

Законы газодинамики важны для современной авиации, разработки паровых и газовых турбин, космической техники и т.д.

Газодинамика, как и аэродинамика, не учитывает конкретное строение газов, рассматривания их как непрерывную среду, распределенную в пространстве. Совокупность частиц, двигающегося газа, называется потоком газа. Течение газа (поток) называется стационарным (установившемся), если параметры потока (скорость, давление, плотность и т.д.) не изменяются с течением времени в каждой точке (сечении) потока.

Рассмотрим процессы, происходящие в газовом потоке с точки зрения законов термодинамики. Пусть имеется стационарный поток газа. На пути потока имеется устройство С, которое превращает энергию потока в работу (например, газовая турбина), или наоборот устройство, которое передает энергию потоку за счет работы внешних сил (например, компрессор) (рис.1).

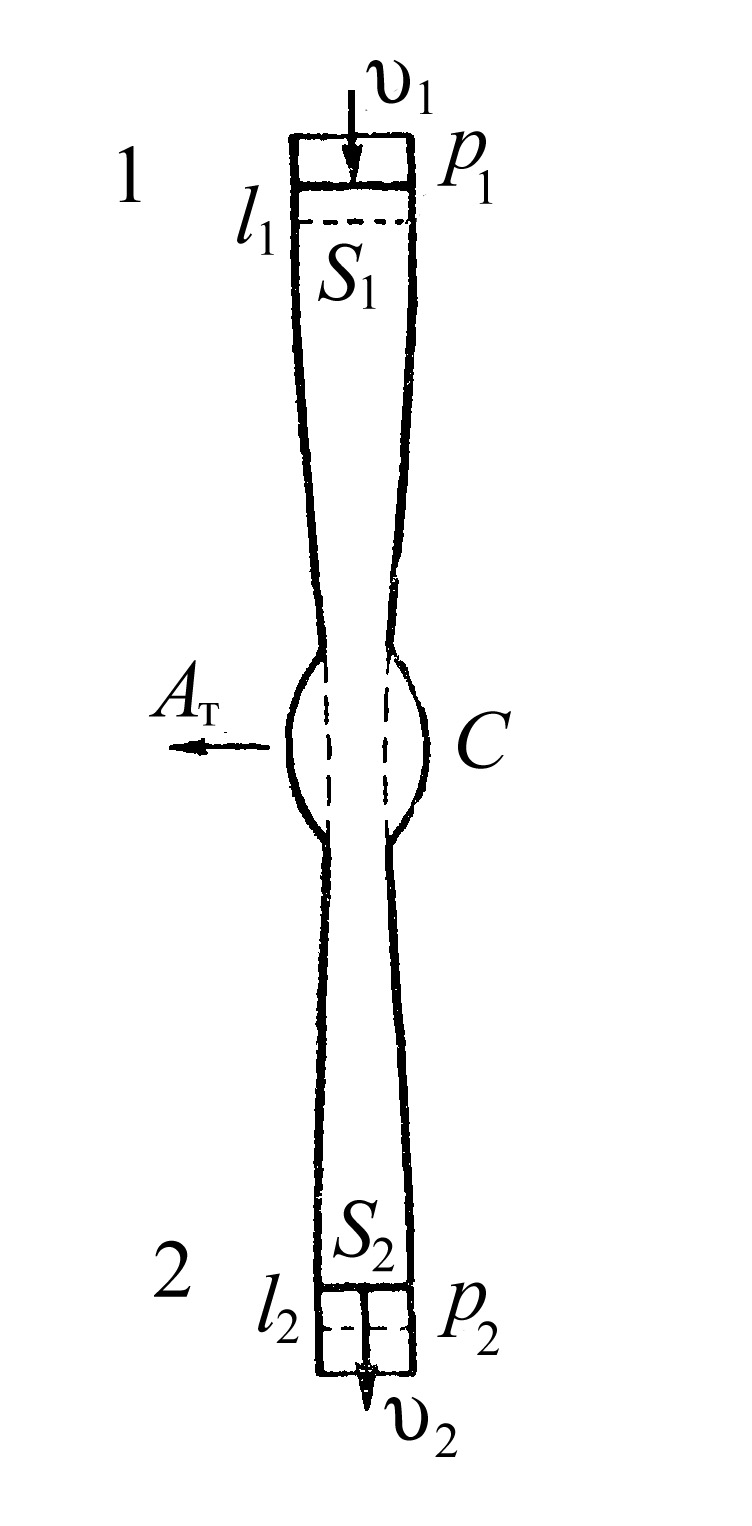
Рис.1 К выводу основного уравнения газодинамики

Так как поток стационарный, то параметры состояния потока в любом сечении остаются постоянными в любой момент времени, хотя для различных сечений (например, 1 и 2) они могут быть различными.

Пусть на участке 1 давление газа p₁, а скорость u₁, а на участке 2 p₂ и u₂ соответственно. За время dt через сечение S₁ протекает объем газа V₁, а через сечение S₂ объем V₂. В случае стационарного потока массы газа протекающие через сечения S₁ и S₂ за время dt должны быть одинаковые (закон сохранения массы):

m₁ = m₂ = m =const

Или r₁V₁ = r₂V₂

Или r₁S₁l₁ = r₂S₂l₂

Окончательно: r₁S₁u₁dt = r₂S₂u₂dt (1)

Отсюда следует, что

ruS = const (2)

(в гидро- и аэродинамике uS = const)

Если dt = 1с, то M = ruS – масса газа, протекающая через сечение S в единицу времени. Эта величина называется расходом газа.

Согласно I началу термодинамики количество теплоты Q переданное выделенной части газового потока (часть 1-2) за время dt равно:

Q = DE + A, (3)

где

DE = DU + DE_к (4)

изменение полной энергии газа, которое складывается из изменения внутренней энергии газа DU и изменения его кинетической энергии DE_к. A – полная работа, которая складывается из работы сил давления на торцевые поверхности выделенной части газового потока A_p, технической работы A_т в устройстве C и работы против сил трения A_тр:

A = A_p + A_т + A_тр (5)

С учетом (4) и (5) уравнение (3) принимает вид:

Q =DU + DE_к +A_p +A_т +A_тр (6)

В (6)

DU = U₂ – U₁ (7)

где U₂ и U₁ – внутренняя энергия газа в сечениях 2 и 1 соответственно,

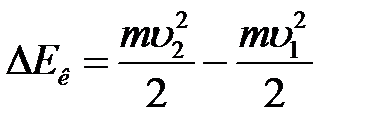(8)

изменение кинетической энергии газа при прохождении через соответствующие сечения.

Работа сил давления на торцевые поверхности:

A_p = A₂ – A₁ = F₂l₂ – F₁l₁ = p₂S₂u₂dt – p₁S₁u₁dt (9)

Учитывая, что udt = l, а Sl = V, получим

A_p = p₂V₂ – p₁V₁ (10)

В сечении 1 работа выполняется над выделенным объемом газа внешними силами (знак “-“, например, поршень сжимает газ до давления p₁). В сечении 2 сам газ выполняет работу, действуя на нижние слои с давлением p₂.

С учетом (7), (8) и (10) уравнение (6) преобразуется к виду:

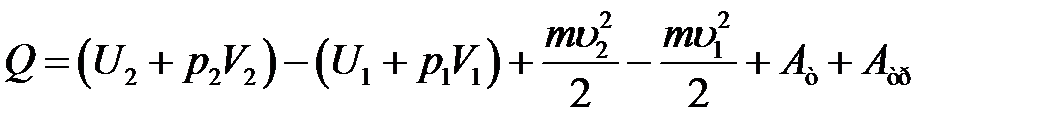(11)

В (11) величина U + pV = I – энтальпия или теплосодержание.

C учетом этого уравнение (11) принимает вид:

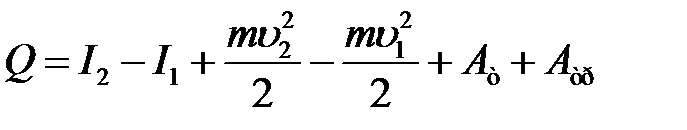(12)

(12) – основное уравнение газодинамики. В реальных тепловых процессах, при нахождении работы, совершенной газовым потоком, эта величина играет большую роль. Она определяет “работоспособность“ газа. На самом деле, если течение газа адиабатное (Q = 0), то из (12) видно, что газовый поток выполняет работу за счет уменьшения энтальпии и кинетической энергии.

Рассмотрим адиабатное течение газа по трубопроводу переменного сечения без совершения технической работы (A_т = 0). Для упрощения не будем учитывать силы трения (A_тр = 0). С учетом этого уравнение (12) принимает вид:

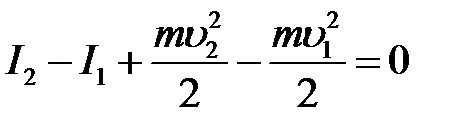
или:

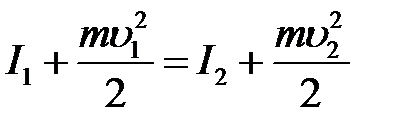
Отсюда следует:

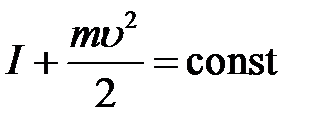(13)

Уравнение (13) – термодинамическое обобщение уравнения Бернулли. Из него следует, что сумма энтальпии и кинетической энергии газового потока при стационарном адиабатном течении газа без выполнения работы одинакова для любого сечения потока.

Преобразуем уравнение (13):

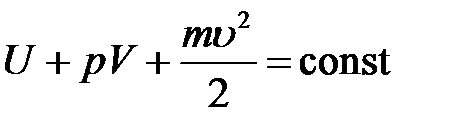
или:

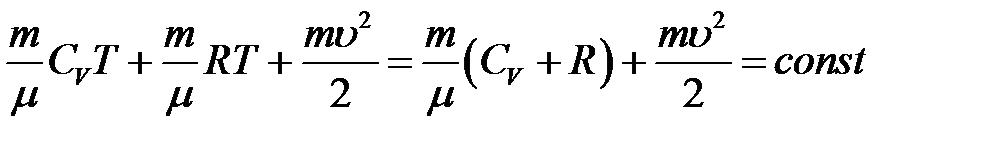
или:

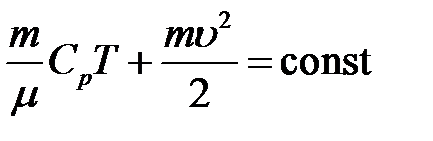
Так как поток стационарный, то через любое поперечное сечение за одно и тоже время проходит одна и та же масса газа, т.е. m = const. Тогда:

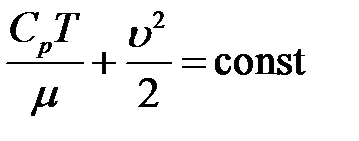(14)

Из (14) следует, что при изменении скорости газа должна изменяться его температура. Для двух сечений газового потока получим:

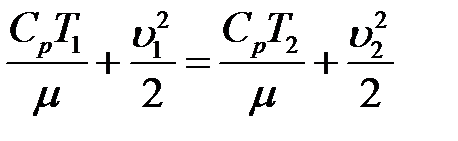
или:

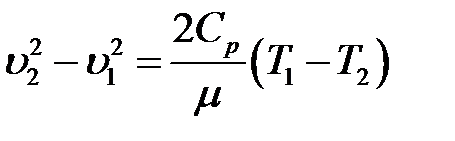
Известно, что:

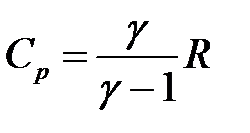
С учетом этого последнее уравнение принимает вид:

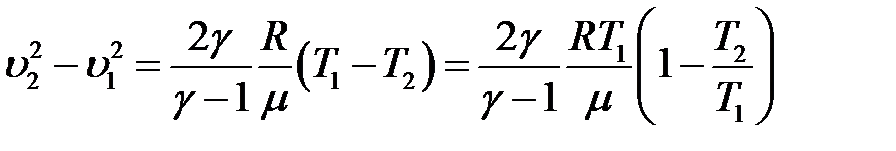(15)

Для адиабатного течения газа справедливо уравнение Пуассона:

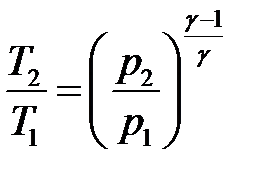
Из уравнения Клапейрона-Менделеева:

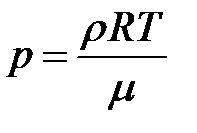
где r - плотность газа. С учетом этого уравнение Пуассона принимает вид:

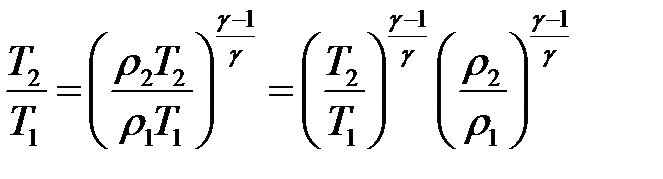
или:

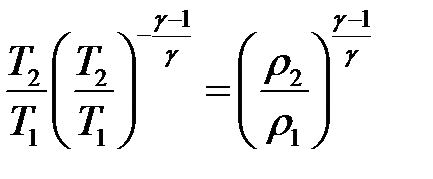
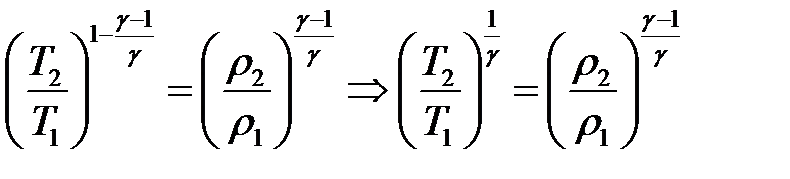
Окончательно:

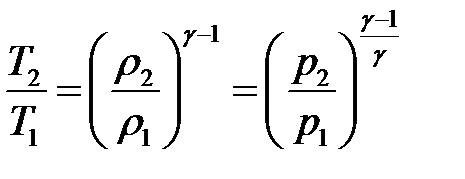(16)

С учетом (16) из (15) получим:

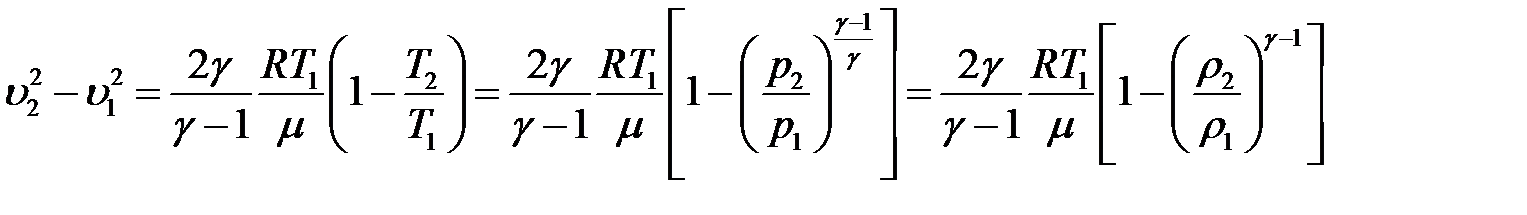(17)

Из (17) вытекает, что если u₂ > u₁, то и T₂ < T₁, p₂ < p₁, r₂ < r₁.

Течение газа, при котором кинетическая энергия потока (скорость) возрастает, а температура, давление и плотность уменьшается, называется течением с расширением (истечение пара из котла, газа из камеры сгорания реактивного двигателя).

Рассмотрим резервуар большого объема с газом под давлением p₁ и температурой T₁ (рис.2).

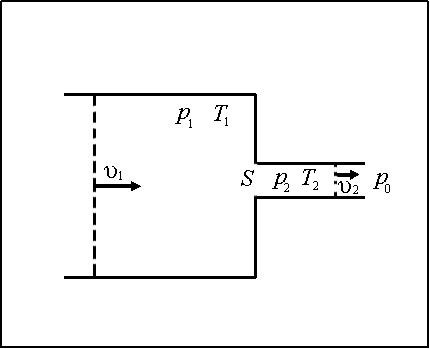
Рис. 2. К определению критической скорости

Пусть газ адиабатно вытекает через отверстие с площадью S в резервуар, где давление p₀ (противодавление). Из-за больших размеров резервуара можно считать, что u₁ = 0. Тогда из уравнения (17) получим:

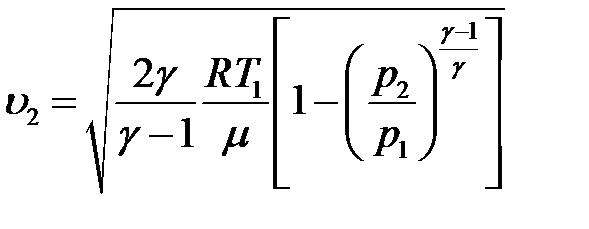(18)

где p₂ – статическое давление в струе газа, вытекающего через отверстие. Если уменьшать противодавление p₀, то будет уменьшаться и давление p₂, а, следовательно, адиабатно будет уменьшаться и плотность r вытекающего газа (уравнение (17)), при этом скорость u₂ будет увеличиваться.

Рассмотрим влияние величины противодавления на расход газа M = ruS.

Очевидно, что расход газа через отверстие постоянной площади определяется двумя величинами: плотностью и скоростью истечения газа. Плотность газа уменьшается с уменьшением противодавления, а скорость истечения наоборот увеличивается. Поэтому расход газа при уменьшении противодавления сначала будет расти за счет быстрого увеличения скорости u₂, однако затем увеличение расхода газа замедляется за счет уменьшения плотности газа и, наконец, станет постоянным.

Дальнейшее уменьшение противодавления p₀ не приводит ни к увеличению скорости потока, ни к увеличению расхода газа. В потоке устанавливаются так называемые критические значения скорости истечения, давления, температуры и плотности газа, которые не изменяются при дальнейшем уменьшении противодавления.

Если до этого момента давление газа на выходе потока было равно противодавлению, т.е. p₂ = p₀, то с этого момента, при истечении газа с критической скоростью в выходном отверстии будет наблюдаться скачок давления p₂ > p₀. Это происходит потому, что дальнейшее уменьшение p₀ уже не приводит к уменьшению p₂.

Можно доказать, что отношение давления в резервуаре p₁ к критическому давлению газа в потоке p_к определяется выражением:

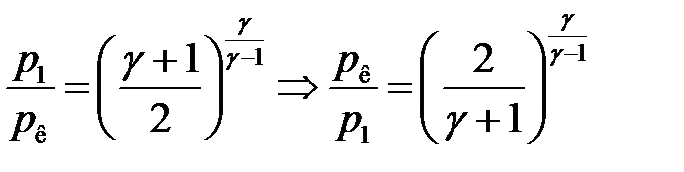(19)

где

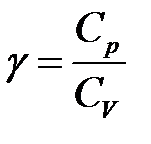
Для воздуха p₁/p_к = 1,89.

Выясним физический смысл критической скорости. При достижении потоком газа критической скорости истечения из (19) получим:

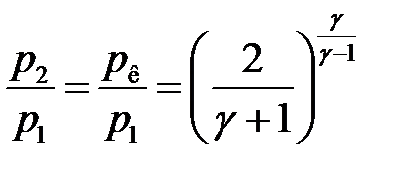
Подставим в (18) и после несложных преобразований получим:

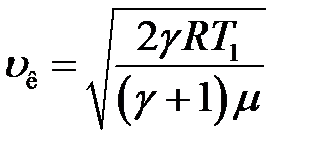(20)

Из уравнения Пуассона с учетом (19) получим:

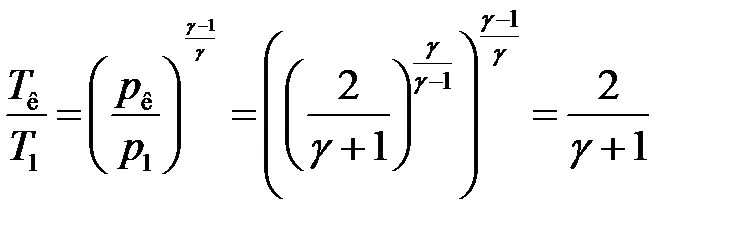
Отсюда:

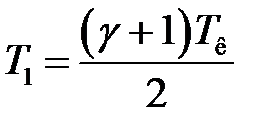
С учетом этого из (20) получим:

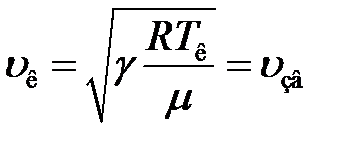(21)

Из (21) видно, что критическая скорость равна скорости распространения звука в газе при температуре потока газа, равной критической температуре.

Каким бы большим не было давление в резервуаре, каким бы маленьким не было противодавление в окружающем пространстве, газ не может вытекать со скоростью большей, чем скорость звука при данной температуре. Когда давление в потоке равно критическому, а скорость истечения равна скорости звука, то расход газа M будет максимально возможным при имеющихся начальных термодинамических параметрах газа в резервуаре (баллоне).

Лекция 25