Дихотомия (метод половинного деления)

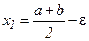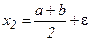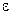Исходный отрезок делится пополам парой измерений: , , где – некоторое заранее заданное достаточно малое число. Вычисляются значения функции в этих точках и сравниваются между собой. Если при поиске минимума 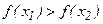, то отрезок 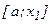заведомо не содержит точку минимуиа и поэтому интервал поиска можно сократить, перенеся его левый конец в точку 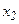. После этого возникает та же, что и ранее, задача, но интервал поиска сокращен (с точностью до ) вдвое. Таким образом осуществляется последовательное деление исходного интервала пополам парами измерений. При этом .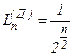

Дихотомия существенно эффективнее, чем шаблонный подход. Так, для сужения интервала в 100 раз нужно 198 пассивных измерений или 14 дихотомий.

Метод Фибоначчи

Число Фибоначчи равно сумме двух предыдущих 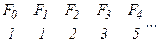. Недостаток метода Фибоначчи – необходимость заранее знать число шагов . , ,

.

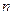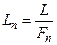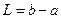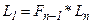На первом шаге симметрично относительно краев интервала строятся точки на расстоянии 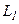, 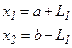. Вычисляются значения функций в этих точках и сравниваются. Аналогично методу Дихотомии производится сужение интервала.

На втором и последующих шагах делается только одно измерение 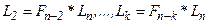, , 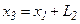есл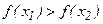и и 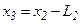, если 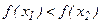. И так далее, до тех пор пока интервал неопределенности не будет меньше ε. В качестве точки минимума выбирается середина отрезка.

Для сокращения интервала в 100 раз требуется всего 11 измерений.