Условия существования экстремума. Аналитические методы решения

Аналитический подход к задаче определения локальных и глобальных минимумов состоит в использовании методов математического анализа для поиска уравнений, которым должны удовлетворять эти точки, и для решения этих уравнений.

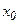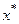Из рисунка 4.2.1 видно, что в точках и касательная к графику функции будет параллельна оси OX, а это означает, что производная функции 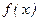в этих точках будет равна нулю. Следовательно, 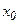и 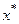будут решениями уравнения .

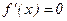Однако это же справедливо и для точки максимума 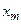, и для точки перегиба 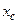. Таким образом, найденное уравнение является необходимым условием минимума, но не является достаточным.

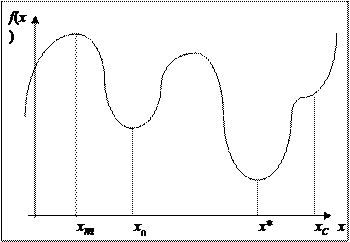Рисунок 4.2.1 - Стационарные точки непрерывной функции

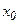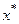В точках и производная 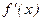меняет знак с отрицательного на положительный, в 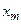- с положительного на отрицательный, в точке 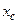производная знак не меняет. Следовательно, в точке минимума производная является возрастающей функцией. Степень же возрастания измеряется второй производной, то есть в нашем случае 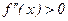, , 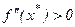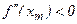. Однако если 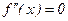, то ситуация остается неопределенной.

Теорема 1(необходимое и достаточное условие существования экстремума функций одной переменной).

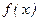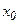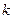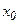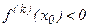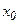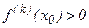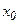Если функция и ее производные непрерывны, то точка является точкой экстремума (максимума или минимума) тогда и только тогда, когда порядок ее первой, не обращающейся в ноль в точке производной есть четное число. При этом, если , то - точка максимума, если , то - точка минимума.

Таким образом, при классическом подходе для поиска минимума функции одной переменной необходимо решить уравнение 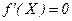и установить знак 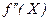в полученных точках. Аналитическое решение такого уравнения в общем случае невозможно, поэтому используются методы приближенного решения уравнения 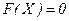, известные из математического анализа (методы Ньютона, бисекций, и т.д.).

Рассмотрим функцию 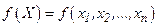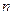действительных переменных. Введем матричные обозначения для точки в 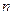-мерном пространстве, градиента (вектора частных производных первого порядка функции 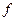) и гессиана (матрицы частных производных второго порядка):

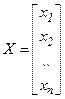- точка в 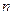-мерном пространстве,

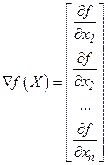- градиент,

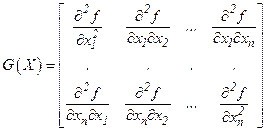- гессиан (матрица Гессе).

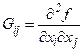- элемент 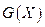- частная производная второго порядка.

Напомним, что 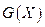- симметрическая матрица.

Предполагая непрерывность 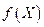и всех ее частных производных, можно обобщить классический подход на случай n³2.

Достаточное условие минимума: 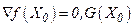- положительно определена.

Достаточное условие максимума: 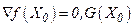- отрицательно определена.

По критерию Сильвестра,

если 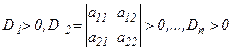– Матрица положительно определена;

если 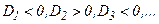– Матрица отрицательно определена.

Пример 1

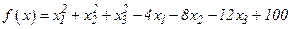
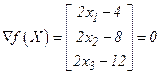, тогда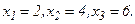

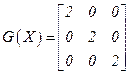положительно определена при любом 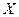, поэтому точка (2, 4, 6) является точкой локального минимума, а так как это единственная стационарная точка, то она же является и точкой глобального минимума.

Таким образом, для решения задачи оптимизации классическим методом необходимо решить систему уравнений 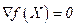, что невозможно сделать аналитически за исключением очень узкого класса таких систем (например, система линейных уравнений невысокого порядка). Затем придется еще устанавливать определенность гессиана, что тоже является совсем нетривиальной задачей в случае больших размерностей. Все это приводит к необходимости разрабатывать итерационные процедуры решения задач оптимизации.