Определение интервала унимодальности

Для определения интервала, содержащего точку минимума, обычно используют следующую процедуру.

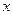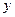Выбирают две стартовые точки и такие, что .

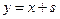Затем, если , определяют следующие точки 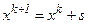до тех пор, пока не будет получено .

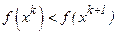В этом случае полученный интервал 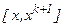«накрывает» искомую точку минимума.

Если же 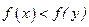, то выбирается противоположное направление. Точки строятся по правилу 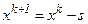до тех пор, пока не будет получено .

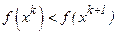Основной проблемой при применении описанной процедуры является правильный выбор величины 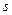. Во многих прикладных задачах переменная изменяется в пределах многих степеней десятки (например, от 0,001 до 10000). Тогда при неправильном выборе величины 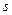минимизация может потребовать слишком больших затрат (при очень малом 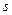- на «накрытие» точки минимума, а при большом - на последующее за «накрытием» сужение отрезка до требуемой точности).

Для того чтобы преодолеть эту проблему, был предложен подход с удвоением шага. В этом случае определение верхней границы интервала осуществляется по правилу .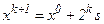

После того, как точка минимума была накрыта, нижняя граница интервала определяется тем же самым процессом, но с изменением знака перед 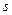и в обратном направлении.

И последнее, что следует здесь учесть - это возможность того, что целевая функция вообще является постоянной. Для учета этого обстоятельства необходимо вводить максимальную длину шага, которая не должна быть превышена в процессе определения отрезка, содержащего точку минимума.