Безусловная одномерная оптимизация

Задачи безусловной одномерной минимизации представляют собой простейшую математическую модель оптимизации, в которой целевая функция зависит от одной переменной, а допустимым множеством является отрезок вещественной оси:

.

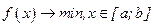К математическим задачам одномерной минимизации приводят прикладные задачи оптимизации с одной управляемой переменной. Кроме того минимизация функций одной переменной является как правило необходимым элементом многих методов минимизации многомерных функция безусловной и условной оптимизации.

На первый взгляд кажется, что задача минимизации функции одной переменной является довольно элементарной. В самом деле, если функция 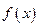, которую нужно минимизировать на отрезке 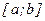, дифференцируема, то достаточно найти нули производной, присоединить к ним концы отрезка, выделить из этих точек локальные минимумы и, наконец, среди последних найти ту точку, в которой достигается абсолютный минимум.

Однако для широкого класса функций эта задача не так уж проста. Во-первых, задача решения уравнения 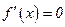может оказаться, как это и бывает в отдельных ситуациях, весьма сложной. С другой стороны, в практических задачах часто не известно, является ли функция дифференцируемой. Ввиду этого существенное значение приобретают методы оптимизации не требующие вычисления производной.

Методы, использующие только значения функции и не требующие вычисления ее производных, называются прямыми методами минимизации. Большим достоинством прямых методов является то, что от целевой функции не требуется дифференцируемости и, более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы прямых методов минимизации, это возможность определения значений 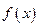в заданных точках. Методами поиска определяется достаточно малый интервал, в котором находится минимум, осуществляя при этом наименьшее количество вычислений функции (так как затраты на вычисления могут быть весьма велики).

Рассмотрим наиболее распространенные на практике прямые методы поиска точки минимума. Так как для приближенного определение точки оптимума исследуют поведение функции в конечном числе точек, то методы отличаются друг от друга лишь способом выбора этих точек. Суть методов состоит в построении последовательности отрезков стягивающихся к точке минимума.

Самым слабым требованием на функцию 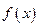, позволяющим использовать эти методы, является ее унимодальность, то есть функция имеет на заданном отрезке только одну точку минимума. Прежде, чем применять эти методы, необходимо выделить интервал, содержащий искомую точку минимума, и убедиться, что она там единственная. В противном случае предлагаемые методы будут определять только один локальный минимум.