Алгоритм 2 (метода подбора)
Пусть требуется найти частное решение уравнения
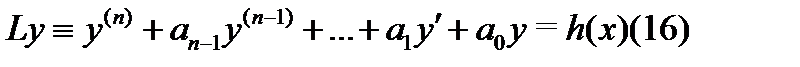
с постоянными коэффициентами 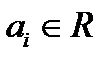 и с неоднородностью
и с неоднородностью 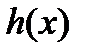 , являющейся квазимногочленом (15). Для этого надо сделать следующее:
, являющейся квазимногочленом (15). Для этого надо сделать следующее:
1) составить спектральное значение 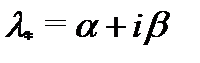 правой части
правой части 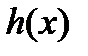 уравнения (16);
уравнения (16);
2) если спектральное значение 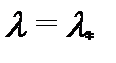 не является корнем характеристического уравнения
не является корнем характеристического уравнения
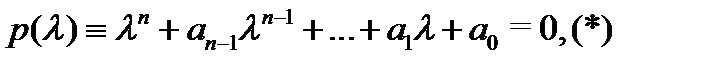
то частное решение следует искать в виде
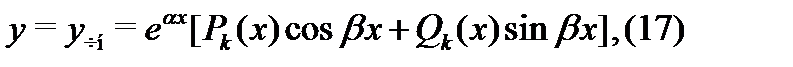
где 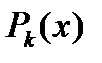 и
и 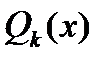 –- многочлены (с неопределенными коэффициентами) степени
–- многочлены (с неопределенными коэффициентами) степени 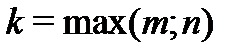 ;
;
3) если спектральное значение 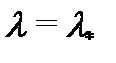 является корнем кратности
является корнем кратности 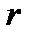 хаpактеристического уравнения
хаpактеристического уравнения  , то частное решение следует искать в виде
, то частное решение следует искать в виде
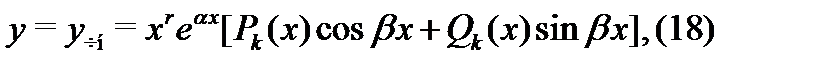
где 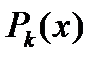 и
и 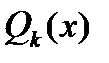 – многочлены (с неопределенными коэффициентами) степени
– многочлены (с неопределенными коэффициентами) степени 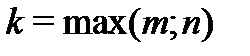 ;
;
4) для вычисления неопределенных коэффициентов надо подставить функцию (17) (или (18)) в уравнение (16), сократить его обе части на экспоненту 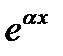 и произвести приравнивание коэффициентов в обеих частях при одинаковых
и произвести приравнивание коэффициентов в обеих частях при одинаковых 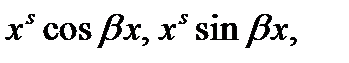 а затем решить полученную линейную систему алгебраических уравнений относительно неопределенных коэффициентов.
а затем решить полученную линейную систему алгебраических уравнений относительно неопределенных коэффициентов.
Заметим, что если спектральное значение 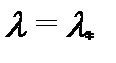 является корнем характеристического уравнения
является корнем характеристического уравнения  , то говорят, что в уравнении (16) имеет место резонанс.
, то говорят, что в уравнении (16) имеет место резонанс.
Мы не будем заниматься обоснованием этого алгоритма. Такое обоснование можно найти во многих учебных пособиях по обыкновенным дифференциальным уравнениям (см., например, [1]). Покажем, как он работает на практике. Отметим, что при применении алгоритма 2 часто используется следующий принцип суперпозиции.
Принцип суперпозиции. Если правая часть 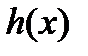 уравнения
уравнения
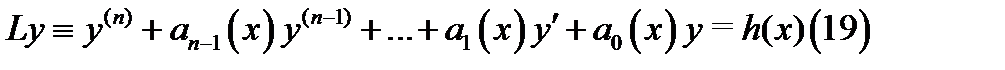
является линейной комбинацией непрерывных на отрезке 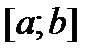 функций
функций 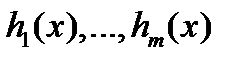 ( т.е. если
( т.е. если 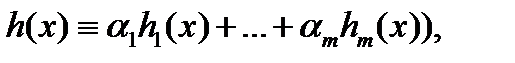 то линейная комбинация
то линейная комбинация 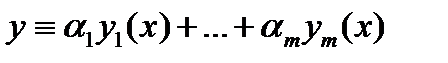 решений
решений 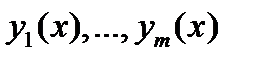 уравнений
уравнений 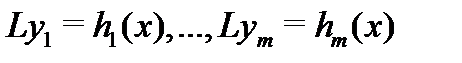 является решением уравнения (19) (здесь числа
является решением уравнения (19) (здесь числа 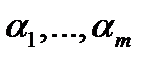 могут быть и комплексными).
могут быть и комплексными).
Действительно, в силу линейности оператора 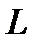 из тождеств
из тождеств
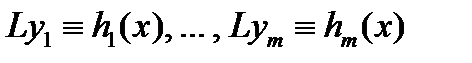
вытекает тождество
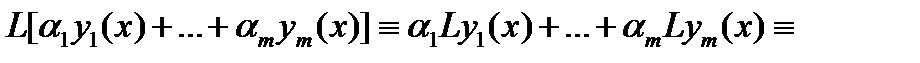
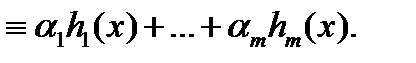
Рассмотрим несколько примеров.
Пример 4. Найти общее решение уравнения
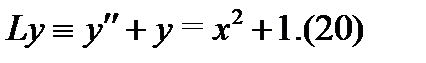
Решение.Так как в правой части (20) нет 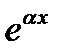 , то
, то 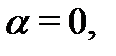 и поскольку в правой части нет синусов и косинусов, то
и поскольку в правой части нет синусов и косинусов, то 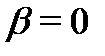 . Значит, спектральное значение правой части равно
. Значит, спектральное значение правой части равно 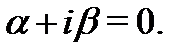 Характеристическое уравнение
Характеристическое уравнение 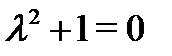 имеет два различных чисто мнимых корня
имеет два различных чисто мнимых корня 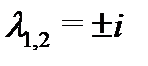 и спектральное значение
и спектральное значение 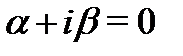 oтличается от них, поэтому частное решение неоднородного уравнения (20) следует искать в виде
oтличается от них, поэтому частное решение неоднородного уравнения (20) следует искать в виде
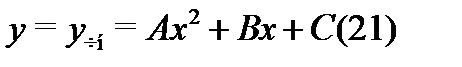
(т.е. в таком же виде, что и правая часть уравнения (20)). Для вычисления неопределенных коэффициентов 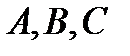 надо подставить (21) в (20) и произвести приравнивание коэффициентов при oдинаковых степенях
надо подставить (21) в (20) и произвести приравнивание коэффициентов при oдинаковых степенях 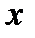 . Вычислим сначала производные от многочлена (21):
. Вычислим сначала производные от многочлена (21): 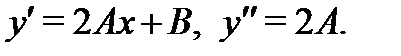 Значит,
Значит, 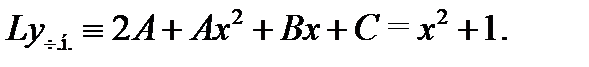 Приравнивание коэффициентов дает:
Приравнивание коэффициентов дает:
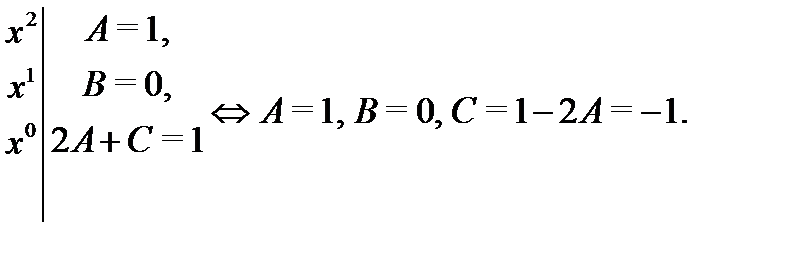
Подставляя найденные коэффициенты в (21), найдем окончательно частное решение неоднородного уравнения (20): 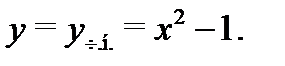 Поскольку корни
Поскольку корни 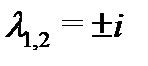 характеристического уравнения
характеристического уравнения  различны, то общее решение соответствующего однородного уравнения имеет вид
различны, то общее решение соответствующего однородного уравнения имеет вид 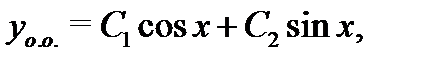 а значит общее решение исходного уравнения (20) запишется в форме
а значит общее решение исходного уравнения (20) запишется в форме 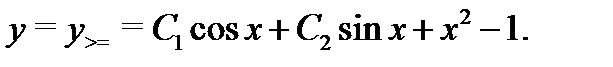
Пример 5. Найти общее решение уравнения
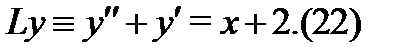
Решение. Найти общее решение соответствующего однородного уравнения 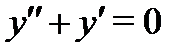 не составляет труда, так как здесь корни характеристического уравнения
не составляет труда, так как здесь корни характеристического уравнения 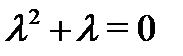 различны:
различны: 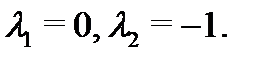 Оно имеет вид
Оно имеет вид 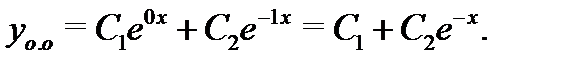 Займемся вычислением частного решения неоднородного уравнения (22). Поскольку в правой части нет экспоненты
Займемся вычислением частного решения неоднородного уравнения (22). Поскольку в правой части нет экспоненты 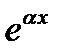 и синусов и косинусов, то спектральное значение
и синусов и косинусов, то спектральное значение 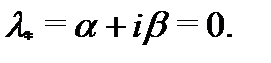 Оно является корнем характеристического уравнения кратности
Оно является корнем характеристического уравнения кратности 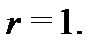 Согласно п.3 алгоритма 2 частное решение неоднородного уравнения (22) следует искать в виде
Согласно п.3 алгоритма 2 частное решение неоднородного уравнения (22) следует искать в виде
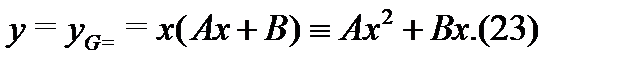
Вычисляя производные 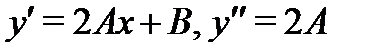 функции (23) и подставляя ее в (22), будем иметь
функции (23) и подставляя ее в (22), будем иметь 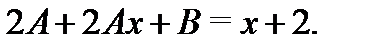 Приравнивая здесь коэффициенты при одинаковых степенях
Приравнивая здесь коэффициенты при одинаковых степенях 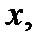 получаем
получаем
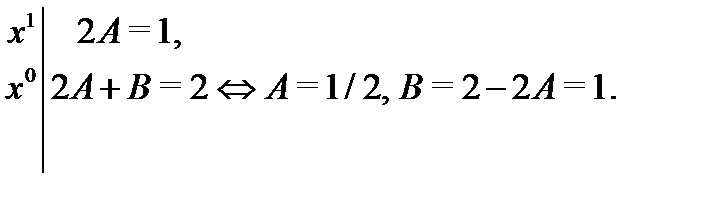
Подставляя 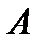 и
и 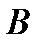 в (23), найдем частное решение уравнения (22) в виде
в (23), найдем частное решение уравнения (22) в виде 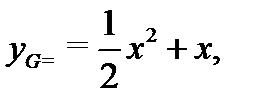 а значит, общее решение этого уравнения запишется в форме
а значит, общее решение этого уравнения запишется в форме
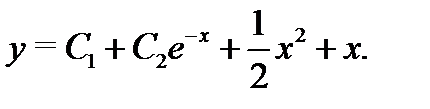
Пример 6.Решить уравнение
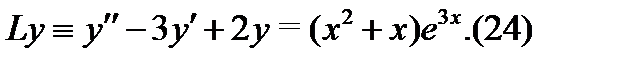
Решение. Спектральное значение правой части 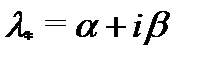 равно
равно 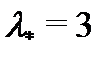 , так как
, так как 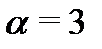 , а синусы и косинусы отсутствуют. Характеристическое уравнение
, а синусы и косинусы отсутствуют. Характеристическое уравнение 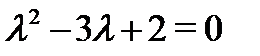 имеет два различных действительных корня:
имеет два различных действительных корня: 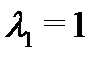 и
и 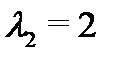 . Так как спектральное значение
. Так как спектральное значение 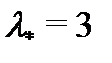 не является коpнем характеристического уравнения, то частное решение уравнения (24) следует искать в виде (см. п.2 алгоритма 2):
не является коpнем характеристического уравнения, то частное решение уравнения (24) следует искать в виде (см. п.2 алгоритма 2):
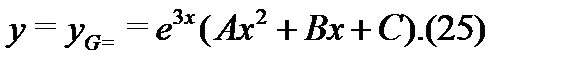
Для составления уравнений относительно неопределенных коэффициентов 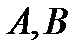 и
и 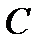 , найдем производные функции (25):
, найдем производные функции (25):
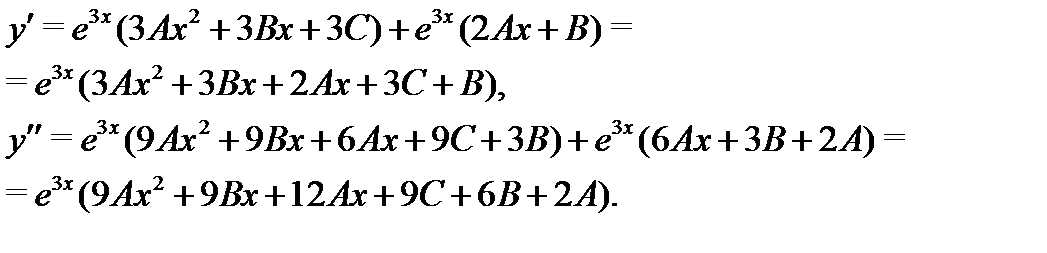
Следовательно,
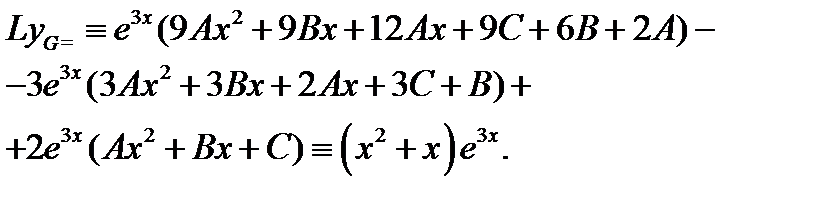
Сокращая здесь экспоненту, получаем тождество
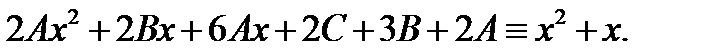
Приpавнивание коэффициентов дает:
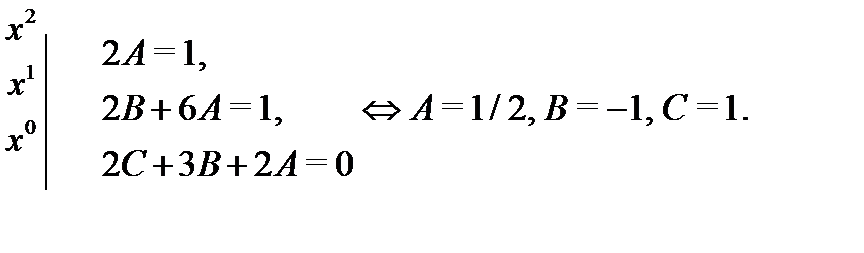
Подставляя 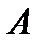 ,
, 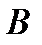 и
и 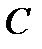 в (25), получаем частное решение в виде
в (25), получаем частное решение в виде 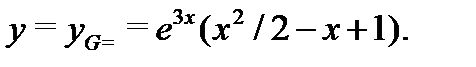 При этом общее решение соответствующего однородного yравнения строится по корням
При этом общее решение соответствующего однородного yравнения строится по корням 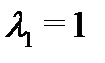 и
и 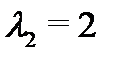 характеристического уравнения следующим образом:
характеристического уравнения следующим образом: 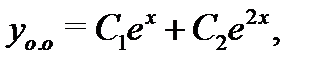 а значит, общее решение неоднoродного уравнения (24) запишется в виде
а значит, общее решение неоднoродного уравнения (24) запишется в виде
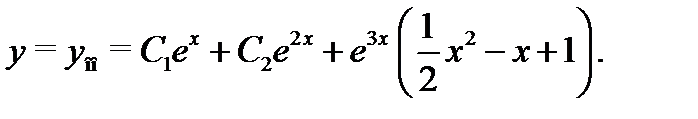
Пример 7. Построить общее решение уравнения
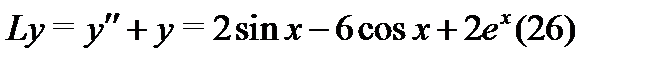
и найти его интегральную кривую, удовлетворяющую начальным условиям 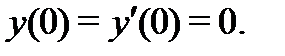
Решение.Здесь правая часть не является квазиполиномом вида (17), поэтому сразу воспользоваться алгоритмом 2 нельзя. Разобьем уравнение (26) на два уравнения
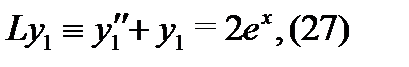
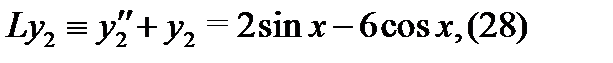
к которым можно применить метод подбора. Если будут найдены частные решения 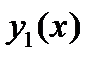 и
и 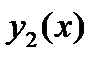 этих уравнений, то, согласно принципу суперпозиции, частное решение исходного уравнения (26) будет иметь вид
этих уравнений, то, согласно принципу суперпозиции, частное решение исходного уравнения (26) будет иметь вид 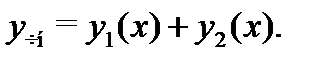
Займемся поиском частного решения уравнения (27). Спектральное значение 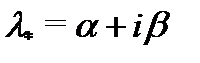 его правой части равно
его правой части равно 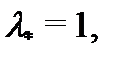 так как в (27) отсутствуют синусы и косинусы. Характеристическое уравнение
так как в (27) отсутствуют синусы и косинусы. Характеристическое уравнение 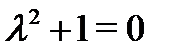 имеет два различных корня
имеет два различных корня 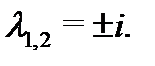 Спектральное значение не совпадает с ними, и поэтому частное решение уравнения (27) следует искать в виде (см. п.2 алгоритма 21)
Спектральное значение не совпадает с ними, и поэтому частное решение уравнения (27) следует искать в виде (см. п.2 алгоритма 21) 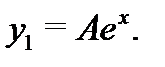 Подставляя это в уравнение (27), имеем
Подставляя это в уравнение (27), имеем 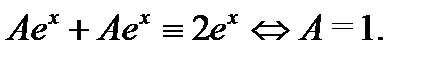 Значит,
Значит, 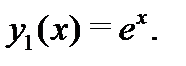
Спектральное значение правой части уравнения (28) равно 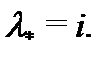 Оно является корнем кратности
Оно является корнем кратности 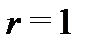 характеристического уравнения, поэтому частное решение уравнения (28) следует искать в виде (см. п.3 алгоритма 2):
характеристического уравнения, поэтому частное решение уравнения (28) следует искать в виде (см. п.3 алгоритма 2): 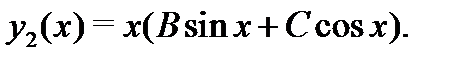 Вычисляя производные
Вычисляя производные
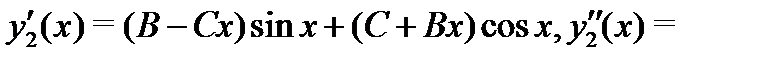
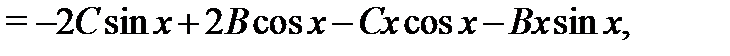
и подставляя их в уравнение (28), получаем тождество
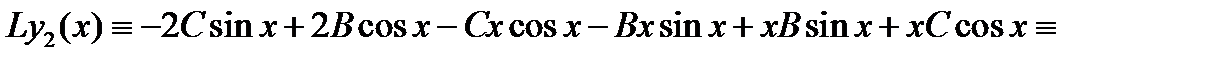
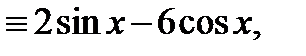
или 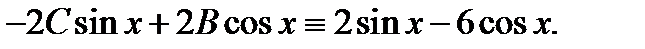 Приравнивая здесь коэффициенты при
Приравнивая здесь коэффициенты при 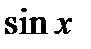 и
и 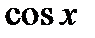 , получаем
, получаем
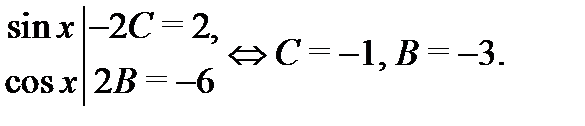
Значит, частное решение уравнения (28) имеет вид 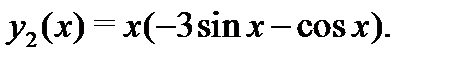 Согласно принципу суперпозиции частное решение уравнения (26) является суммой частных решений
Согласно принципу суперпозиции частное решение уравнения (26) является суммой частных решений 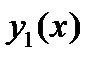 и
и 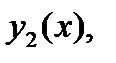 т.е.
т.е. 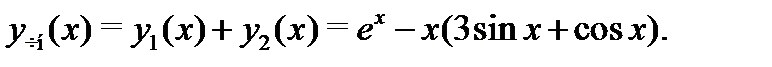
Пo корням 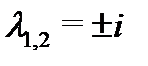 характеристического уравнения
характеристического уравнения  строим общее решение соответстующего однородного уравнения
строим общее решение соответстующего однородного уравнения 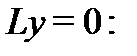
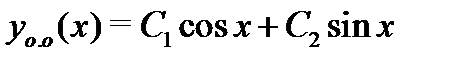 и общее решение исходного неоднородного уравнения (28):
и общее решение исходного неоднородного уравнения (28):
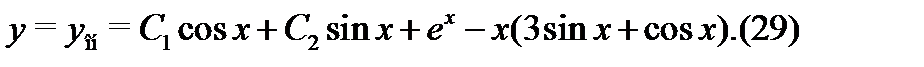
Найдем теперь интегральную кривую, удовлетворяющую начальным условиям 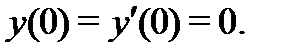 Дифференцируя (29), найдем, что
Дифференцируя (29), найдем, что
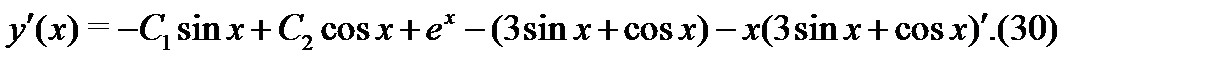
Подчиняя (29) и (30) начальным условиям 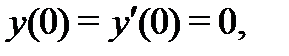 будем иметь
будем иметь
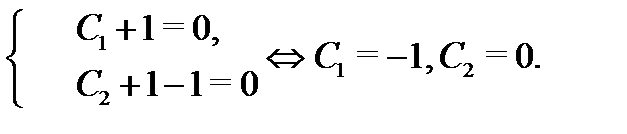
Cледовательно, искомая интегральная кривая задаётся уравнением
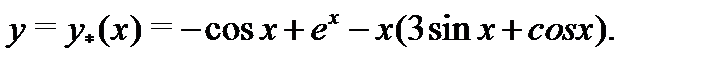
Замечание. Частное решение уравнення (26) можно вычислить с помощью интеграла (см.  ):
): 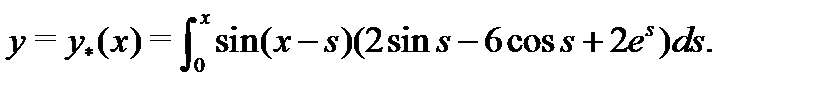
Дата добавления: 2016-06-05; просмотров: 2833;











