Замена переменных в неопределенном интеграле (метод подстановки).

Только что рассмотренный прием подведения под знак дифференциала является частным случаем метода замены переменных и используется, в основном, тогда, когда в подынтегральном выражении легко выделить дифференциал некоторой функции и «узнать» в получившемся после выделения дифференциала выражении табличный интеграл относительно этой функции. Если же в уме подобные преобразования произвести трудно, используют замену переменных. Суть метода в следующем.

Пусть требуется вычислить интеграл 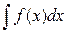, но непосредственно подобрать первообразную для f(x) не удается, хотя известно, что она существует. Заменим переменную интегрирования, положив х = j(t) , где j(t) непрерывная функция, имеющая обратную t = j^–1(x), тогда dх = j¢(t)dt и имеет место равенство

= ,

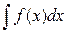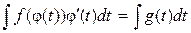где g(t) = f(j(t))j¢(t).

Если для функции g(t) первообразную найти нетрудно и она равна G(t) , то согласно свойству 6, имеем

= .

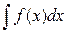Рассмотрим примеры.

Пример3.

.

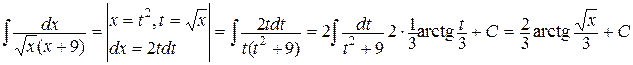При интегрировании методом замены переменных иногда удобнее подбирать подстановку в виде t = j(x), но при этом необходимо, чтобы в заданном подынтегральном выражении f(x)dx можно было легко получить множитель вида j¢(x)dx, дающий дифференциал новой переменной t .

Пример4.

а) .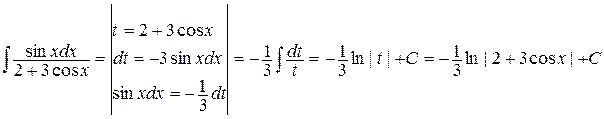

Заметим, что этот интеграл можно вычислить и подведением под знак дифференциала, если учесть, что .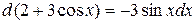

б)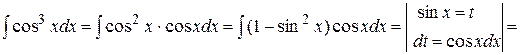

.

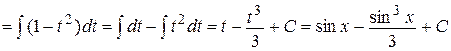Выбор правильной подстановки зависит от навыка и интуиции вычислителя. Если выбор окажется не совсем удачным, замену переменных можно применять несколько раз, пока не будет получен результат. В некоторых часто встречающихся ситуациях можно дать определенные рекомендации (здесь и в дальнейшем буквой R будем обозначать рациональную функцию соответствующих аргументов):

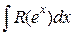– используется подстановка t = e^x

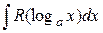– используется подстановка t = log_ax.

В дальнейшем мы рассмотрим еще некоторые классы интегралов, в которых используются вполне конкретные подстановки.