Метод дихотомии (бисекций).

Иначе называется методом половинного деления. Пусть задан начальный интервал [x₀, x₁], на котором f(x₀)f(x₁) ≤ 0 (т.е. внутри имеется не менее чем один корень). Найдем x₂ = ½ (x₀ + x₁) и вычислим f(x₂). Если f(x₀)f(x₂) ≤ 0, используем для дальнейшего деления отрезок [x₀, x₂], если > 0 – используем для дальнейшего деления отрезок [x₁, x₂], и продолжаем деление пополам.

Итерации продолжаются, пока длина отрезка не станет меньше 2ξ ­– заданной точности. Тогда середина последнего отрезка даст значение корня с требуемой точностью. В качестве иного критерия можно взять | f(x)| ≤ ξ_y.

Скорость сходимости метода невелика, однако он прост и надежен. Метод неприменим к корням четной кратности. Если на отрезке несколько корней, то заранее неизвестно, к какому из них сойдется процесс.

Если на заданном интервале предполагается несколько корней, то существует возможность последовательно исключать найденные корни из рассмотрения. Для этого воспользуемся вспомогательной функцией 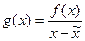, где 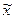– только что найденный корень. Для функций f(x) и g(x) совпадают все корни, за исключением 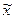(в этой точке полюс функции g(x)). Для достижения требуемой точности рекомендуется грубо приблизиться к корню по функции g(x), а затем уточнить его, используя f(x).

Метод хорд.

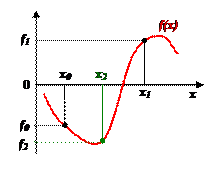
Идея метода проиллюстрирована рисунком. Задается интервал [x₀, x₁], на котором f(x₀)f(x₁) ≤ 0, между точками x₀ и x₁ строится хорда, стягивающая f(x). Очередное приближение берется в точке x₂, где хорда пересекает ось абсцисс. В качестве нового интервала для продолжения итерационного процесса выбирается тот, на концах которого функция имеет разные знаки. Условия выхода из итерационного цикла: 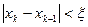или

| f(x)| ≤ ξ_y.

Для вывода итерационной формулы процесса найдем точку пересечения хорды (описываемой уравнением прямой) с осью абсцисс: ax₂ + b = 0, где 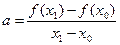; b = f(x₀) ­­– ax₀.

Отсюда легко выразить .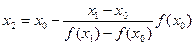

Метод хорд в большинстве случаев работает быстрее, чем метод дихотомии. Недостатки метода те же, что и в предыдущем случае.