Задача аппроксимации функций

Вычисление значения функции 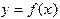- одна из тех задач, с которой приходится постоянно сталкиваться на практике. Часто непосредственное вычисление затруднено, либо приводит к слишком большим затратам машинного времени. Вот некоторые типичные ситуации:

· Функция задана таблицей своих значений

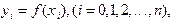(3.1)

а вычисления производятся в точках 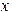, не совпадающих с табличными.

· Непосредственное вычисление значения 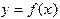связано с проведением сложных расчетов и приводит к значительным затратам машинного времени, которые могут оказаться неприемлемыми, если функция вычисляется многократно.

· При заданном значении 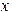значение 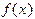может быть найдено из эксперимента. Ясно, что такой способ “вычисления” в большинстве случаев нельзя использовать в вычислительных алгоритмах, так как он связан с необходимостью прерывания вычислительного процесса для проведения эксперимента (такое прерывание естественно при работе в режиме реального времени, например, при управлении технологическим процессом, сложной технической системой, или если компьютер включен в систему обработки данных эксперимента). В такой ситуации экспериментальные данные получают до начала расчетов. Нередко они представляют собой таблицу типа (3.1) с той разницей, что табличные значения отличаются от “истинных”, так как заведомо содержат ошибки эксперимента.

Возникающие проблемы нередко удается решить следующим образом. Функцию 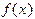приближенно заменяют другой функцией 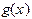, вычисляемые значения которой и принимают за приближенные значения функции 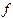. Так решается задача аппроксимации (или приближения) одной функции с помощью другой. Очень часто в качестве аппроксимирующей функции 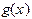выбирают многочлены какой-либо степени ( ).

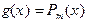Пусть в точках 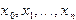, расположенных на отрезке 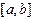, задана таблица (3.1) значений некоторой функции 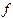. Задача интерполяции состоит в построении функции 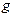, удовлетворяющей условию

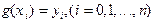. (3.2) Указанный способ приближения функций принято называть интерполяцией, а точки 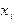- узлами интерполяции. Если 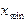, 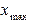- минимальный и максимальный из узлов интерполяции, отрезок 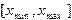называют отрезком наблюдения. Ясно, что выбор функции 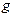далеко не однозначен, хотя на практике используют, как правило, достаточно узкий класс функций, в котором гарантируется единственность выбора. Среди распространенных методов можно назвать использование интерполяционных многочленов Лагранжа, Ньютона, интерполяцию кубическими сплайнами и так далее. Подробно об этих методах можно прочитать в [1].

В случае, когда аппроксимация используется для приближенного значения функции 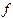в точке, лежащей за пределами отрезка наблюдения, принято говорить, что осуществляется экстраполяция. Этот метод приближения часто используют с целью прогнозирования характера протекания тех или иных процессов при значениях параметров 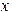, выходящих за пределы отрезка 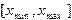. Надежность такого прогноза, очевидно, уменьшается с удалением 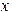на значительное расстояние от отрезка наблюдения, и точность, как правило, невелика.