Метод простой итерации

В рассмотренных выше методах для решения уравнения (1.1) строилась последовательность приближений, которая сходится к корню уравнения. Такие последовательности называются итерационными. Наряду с методом Ньютона и методом секущих получили широкое распространение и другие методы, в частности метод простой итерации. Чтобы применить метод простой итерации для решения уравнения (1.1), необходимо преобразовать это уравнение к виду

(1.5)

Рис.5

Это приведение к виду, удобному для итераций, можно выполнить разными способами (например 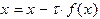, где 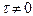- действительное число).

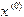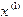Выберем каким-либо образом приближенное значение корня и подставим его в правую часть уравнения (1.5). Получим значение . Подставляя затем в правую часть уравнения (1.5), получим . Продолжая описанные действия таким образом и дальше, находим последовательность приближений по формуле

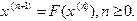(1.6)

На рис.5 показана геометрическая интерпретация метода простой итерации. Корень уравнения (1.4) есть абсцисса точки пересечения графиков функци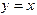й и 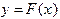. Пусть 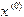- начальное приближение. Так как 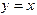-график прямой, проходящей под 45^о к осям координат, то по построению ясно,

что . Построенная таким образом итерационная последовательность сходится к корню 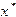уравнения (1.5).

Сходимость

Рассматривая итерационные методы решения нелинейных уравнений, мы оставили в стороне вопрос о сходимости итерационных последовательностей. Ведь вполне может получиться так, что 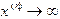при 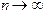. При реализации алгоритма на компьютере это приведет к типичной ошибке (переполнение с плавающей точкой) и программному прерыванию. Для выяснения условий сходимости служит следующая теорема:

Пусть в некоторой окрестности корня 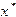уравнения (1.5) функция 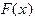дифференцируема и удовлетворяет неравенству

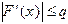, (1.7)

где 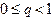- некоторая постоянная величина. Тогда независимо от выбора начального приближения из указанной окрестности корня итерационная последовательность не выходит из этой окрестности, метод (1.6) сходится со скоростью геометрической прогрессии, и справедлива следующая оценка погрешности: .

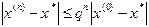Замечание. Для практического применения метода простой итерации и выбора начального приближения часто используют условие .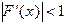

Пример.Пусть необходимо найти положительный корень уравнения 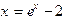. Как видно, производная правой части этого уравнения больше единицы для положительных 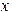, и метод простой итерации приведет к расходящейся последовательности. Тогда исходное уравнение необходимо преобразовать так, чтобы удовлетворить условию сходимости. В данном случае, например, можно представить его в виде .

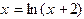Отсюда легко выводится аналогичное условие сходимости для метода Ньютона. Сравнивая формулы (1.2) и (1.6), можно представить решение уравнения (1.1) методом Ньютона как решение уравнения (1.5) методом простой итерации с функцией 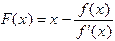. Дифференцируя эту функцию, получим, что 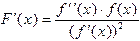. Таким образом, условие сходимости для метода Ньютона выглядит как .

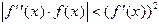Для реализации итерационных методов приближенного решения нелинейных уравнений остается лишь запрограммировать формулы (1.2), (1.3), (1.4) или (1.6) получения последовательных приближений. Рекомендуется использовать цикл repeat...until, причем выход из цикла осуществить при выполнении условия , где 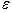-заданная точность.