Численное решение систем линейных уравнений
Методы решения систем линейных алгебраических уравнений разбиваются на две группы. К первой относятся так называемые прямые (или точные) методы - алгоритмы, позволяющие за конечное число арифметических действий получить решение системы. Сюда относится известное правило Крамера нахождения решения с помощью определителей и метод Гаусса (метод исключения). Вторую группу составляют приближенные методы, в частности итерационные методы решения систем уравнений.
Метод Гаусса используется при решении на ЭВМ систем порядка до 103 (правило Крамера применять при этом просто немыслимо). Итерационными методами решаются системы порядка до 106. При этом строятся последовательности 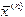 , сходящиеся при
, сходящиеся при 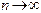 к решению системы. При заданной точности можно считать
к решению системы. При заданной точности можно считать 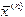 решением, если
решением, если 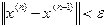 .
.
Метод Гаусса
Рассмотрим систему уравнений N-го порядка:
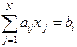 , где
, где 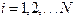 . (2.1)
. (2.1)
В матричном виде эта система записывается в виде 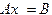 . Метод Гаусса изучался в курсе высшей математики, и напомним, что основная идея метода заключается в следующем.
. Метод Гаусса изучался в курсе высшей математики, и напомним, что основная идея метода заключается в следующем.
1. Прямой ход метода Гаусса: исключая 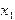 из всех уравнений, кроме первого, получаем в первом столбце коэффициентов матрицы нули во всех строках, кроме первой. Затем исключаем
из всех уравнений, кроме первого, получаем в первом столбце коэффициентов матрицы нули во всех строках, кроме первой. Затем исключаем 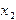 из всех уравнений, кроме первого и второго. Продолжая эти действия дальше, исключаем
из всех уравнений, кроме первого и второго. Продолжая эти действия дальше, исключаем 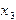 ,
, 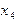 ,... и приходим, наконец, к матрице треугольного вида.
,... и приходим, наконец, к матрице треугольного вида.
2. Обратный ход метода Гаусса: последовательно исключаются 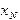 из (N-1)-го уравнения,
из (N-1)-го уравнения, 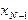 из (N-2)-го уравнения и т.д. Это приводит к диагональному виду матрицы коэффициентов и, соответственно к решению задачи.
из (N-2)-го уравнения и т.д. Это приводит к диагональному виду матрицы коэффициентов и, соответственно к решению задачи.
Для составления программы, реализующей метод Гаусса, удобно пользоваться приведенными ниже формулами. Здесь вводятся вспомогательные матрица C размерности 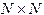 и вектор Y, состоящий из N элементов.
и вектор Y, состоящий из N элементов.
Сначала для прямого хода в цикле для К от 1 до N необходимо вычислять
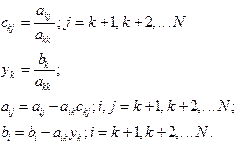 (2.2)
(2.2)
Затем обратный ход метода позволяет получить решение в виде 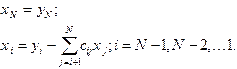 (2.3)
(2.3)
Замечание 1. Может случиться так, что во время вычислений встретился ведущий элемент ( 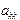 ), равный нулю. Это приведет к ошибке и программному прерыванию (деление на нуль). Такое бывает, например, в том случае, когда исходная система вырождена, то есть ее главный определитель равен нулю, и тогда либо решения нет, либо существует бесконечное множество решений.
), равный нулю. Это приведет к ошибке и программному прерыванию (деление на нуль). Такое бывает, например, в том случае, когда исходная система вырождена, то есть ее главный определитель равен нулю, и тогда либо решения нет, либо существует бесконечное множество решений.
Замечание 2. Даже если главный определитель системы ненулевой, ведущий элемент может оказаться равным нулю, что опять приведет к ошибке. Поэтому рекомендуется применять модификацию метода Гаусса - алгоритм с выбором главного элемента. В этом случае на каждом шаге матрица коэффициентов преобразуется так, чтобы на месте ведущего элемента оказывался наибольший по абсолютной величине элемент строки. Кроме гарантии от ошибки применение метода с выбором главного элемента может существенно уменьшить погрешность вычислений.
Замечание 3. Количество арифметических действий в методе Гаусса растет с увеличением порядка системы 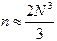 .
.
Дата добавления: 2021-09-07; просмотров: 404;











