Аналитическое описание булевых функций

На примерах описания ФАЛ, приведенных в таблице 3, видно, что конституента 1 может быть описана в виде элементарной конъюнкции переменных:

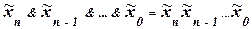; (15)

где: 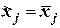,если соответствующий разряд кода равен 0; 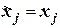,если соответствующий разряд кода равен 1.

Конституента 0 может быть описана в виде элементарной дизъюнкции переменных:

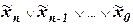; (16)

где: 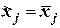,если соответствующий разряд кода равен 1; 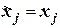,если соответствующий разряд кода равен 0.

Формулы (15) и (16) представляют аналитическую форму записи конституент, как функций алгебры логики.

ФАЛ общего вида может быть аналитически записана:

- в совершенной дизъюнктивной нормальной форме (СДНФ)

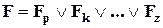; (17)

где F_p , F_k ,..., F_z - конституенты 1. В контексте аналитической записи ФАЛ в СДНФ все конъюнктивные термы имеют максимальный ранг и называются минтермами ранга n.

- в совершенной конъюнктивной нормальной форме (СКНФ)

Ф = Ф_d & Ф_t & ... Ф_y; (18)

где Ф_d , Ф_t ,..., Ф_y - конституенты 0. В контексте аналитической записи ФАЛ в СКНФ все дизъюнктивные термы имеют максимальный ранг и называются макстермами ранга n.

ФАЛ общего вида, приведенная в таблице 3, записывается в СДНФ как:

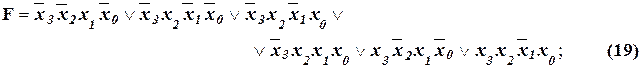В СКНФ эта же ФАЛ записывается как:

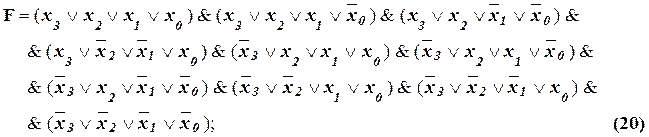Для практического применения обычно используется СДНФ и мы в дальнейшем будем пользоваться только этой формой представления ФАЛ.