Алгоритмы распознавания образов: метод k ближайших соседей, алгоритм «голосования». Метод потенциальных функций и построения разделяющей гиперповерхности. Алгоритм Айдарханова.

1. Метод k ближайших соседей. Предложен в середине 1960-х гг. братьями Зенкиными. Выборку помещают в пространство главного компонента. Смотрят, сколько и каких у каждой точки ближайших соседей.

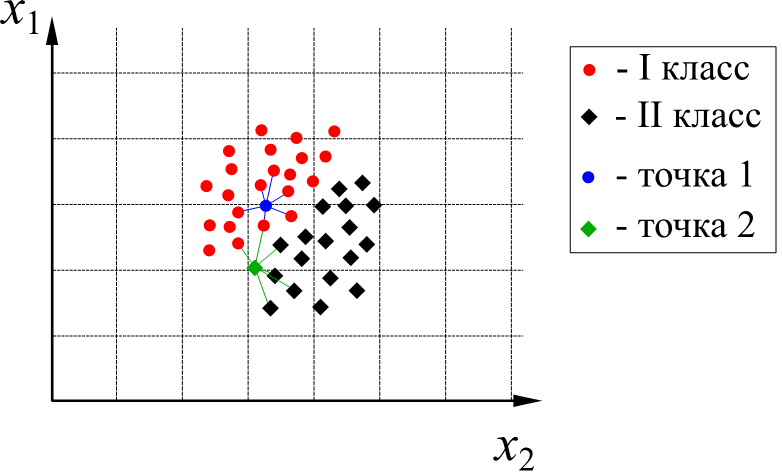
Если число ближайших соседей одного класса превышает число ближайших соседей другого, то точка относится к первому классу. Общее число соседей одного соединения ограничивается k. Не рекомендуется брать k маленьким. Обычно исходят из того что k = 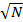, где N - число соединений в выборке.

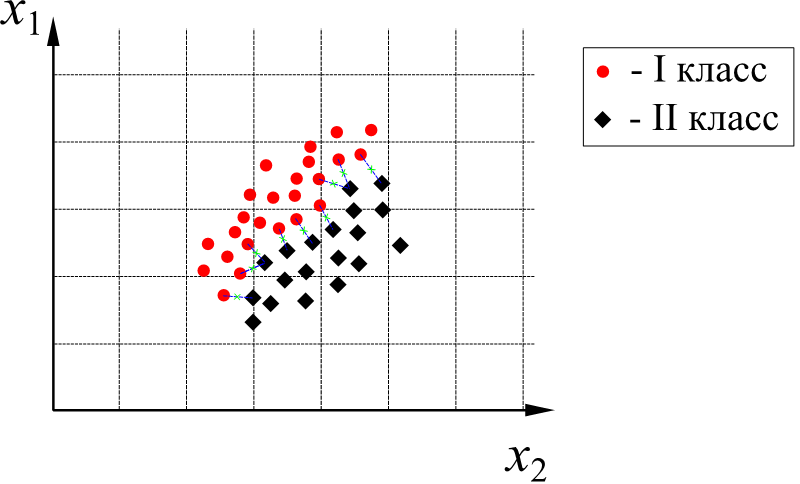
(В приведённом на рисунке примере 41 точка. Тогда 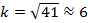. У точки 1 (синяя) все 6 ближайших соседей относятся к I классу, следовательно, и сама точка 1 относится к I классу. У точки 2 (красная) 2 ближайших соседа относятся к I классу, а 4 – ко II классу. Следовательно, точка 2 относится ко II классу.)

После первого распознавания на обучающей выборке вычисляют ошибки первого и второго рода, определяют качество классификации. k варьируют. Проводят аналогичные процедуры, и снова определяют качество. Если качество получается выше предыдущего, то классификация принимается за лучшую.

2. Алгоритм «голосования». Так же предложен братьями Зенкиными. Изначальное факторное пространство переводят в пространство главных компонент. Выбирают некоторое значение ε. В данном пространстве для каждой точки строится сфера радиуса ε. Смотрят, сколько точек разных классов попало внутрь данной окрестности. Если среди точек, попавших в окрестность рассматриваемой, преобладают точки одного класса, то рассматриваемая точка так же относится к этому классу.

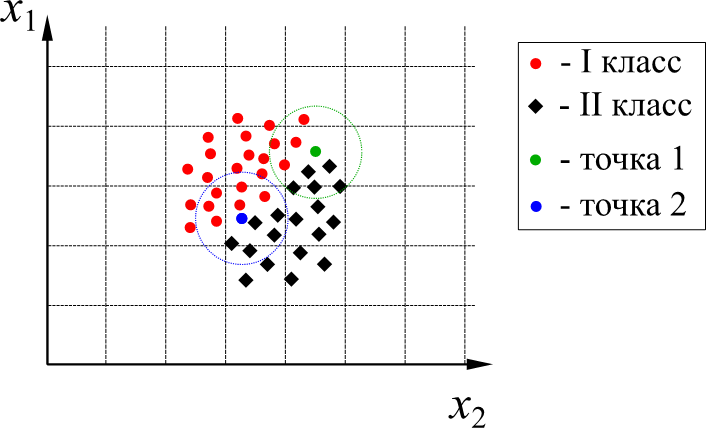
Вычисляют качество классификации, варьируют ε до достижения наилучшего качества.

(В приведённом на рисунке примере в снова оценивается отнесение двух точек – точки 1 (зелёная) и точки 2 (синяя). В ε-окрестность точки 1 (показана зелёным пунктиром) попадают 4 точки I класса и 5 точек II класса. Следовательно, точка 1 относится ко II классу. В то же время, в ε-окрестность точки 2 (показана синим пунктиром) попадают 6 точек I класса и 5 точек II класса. Следовательно, точка 2 относится к I классу.)

3. Метод потенциальных функций. Предложен Р. Мучником. Общая идея метода иллюстрируется на примере электростатического взаимодействия элементарных частиц. Известно, что потенциал электрического поля элементарной заряженной частицы в некоторой точке пространства пропорционален отношению заряда частицы Q к расстоянию до частицы R:

φR =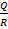

При классификации объект проверяется на близость к объектам из обучающей выборки. Считается, что объекты из обучающей выборки «заряжены» своим классом, а мера «важности» каждого из них при классификации зависит от его «заряда» и расстояния от классифицируемого объекта. Т.е., для любой новой точки отнесение к тому или иному классу производится на основании того, к какому классу она сильнее «притягивается». В качестве потенциальной функции обычно используют степенные функции, реже –экспоненциальные. Это связано с тем, что при расчёте экспоненциальных функций на ЭВМ они раскладываются в ряд Тейлора – степенной ряд.

В МПФ чаще используют функции следующего вида:

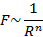
Для каждой точки рассчитывают расстояние до соседних точек данного класса:

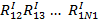
Задают вид функции:

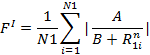
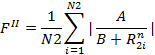
Если F^I > F^II, то соединения относятся к I классу. Для увеличения качества распознавания варьируют параметры A, B и n.

4. Метод построения разделяющей гиперповерхности. Метод предложен В. Н. Вапником. Основан на предположении, что между некомпактными классами можно провести гиперповерхность, оптимально разделяющую каждую пару точек, относящихся к разным классам.

Компактные классы – множества, в которых расстояния между любыми 2 точками, принадлежащими одному множеству, меньше, чем расстояние между любыми точками, относящимися к разным множествам:

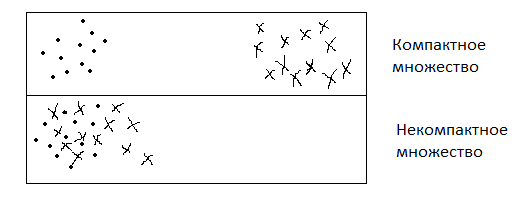
Для построения разделяющей гиперповерхности между каждой парой приграничных точек разных классов строят отрезки. Середины этих отрезков образуют область, идеально разделяющую каждую пару точек.

Далее используется регрессия и осуществляется поиск некоторой поверхности, проходящей среди этих точек. Таким образом, получают уравнение разделяющей гиперповерхности.

5. Алгоритм Айдарханова. Производят обучение на обучающей выборке по 4 алгоритмам. Каждая точка характеризуется следующими параметрами:

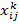, где k – номер класса; I – номер алгоритма; j – номер точки.

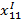– сколько ближайших соседей 1 класса входят в k для 1-й точки.

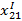– сколько точек 1 класса входят в ε-окрестность 1-й точки.

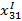– сила, действующая со стороны 1 класса на 1-ю точку.

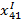– угол, образуемый 1-й точкой относительно 1 класса.

Получаем набор параметров:

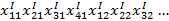
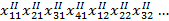
Таким образом, требуется определить оптимальную совокупность алгоритмов, обеспечивающую отнесение точки к её истинному классу.

Определяют обобщённую близость к 1 и 2 классам:

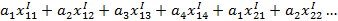
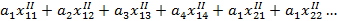
Получаем систему неравенств:

Решают неравенства, подбирая коэффициенты a_i. Однозначного решения такой системы неравенств нет, поэтому далее проводят оптимизацию по расположению объекта.

Качество каждого алгоритма выражается величиной коэффициента a_i.

Алгоритмы распознавания образов: метод главных компонент. Формирование матриц расстояний, определение осей нового пространства. Информационные веса объектов и факторов. Алгоритм «идеального эталона».

Метод главных компонент. Введём следующие обозначения:

R – совокупность (множество) расстояний внутри класса. R должно быть минимальным для наилучшего разделения.

Q – расстояния между точками разных классов. Для наилучшего распознавания Q должно быть максимальным.

Требуется произвести нелинейное преобразование пространства. Для получения компактных классов необходимо, чтобы:

Q – R à max

Q + R à max

Пусть R^I – матрица расстояний внутри класса I. Элементом матрицы R является r_ij – расстояние от точки I до точки j.

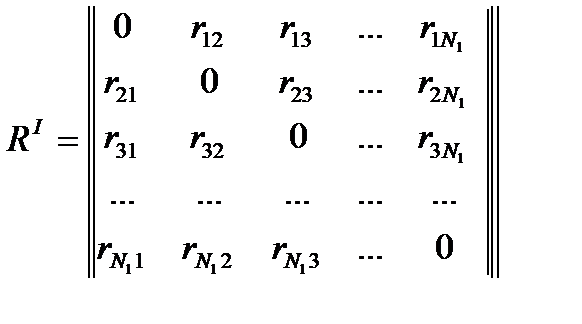
Расстояние определяется как обычная евклидова близость в данном пространстве. Например:

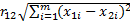, где m – размерность пространства.

Далее формируется матрица Q для класса I, элементами которой являются расстояния от точек класса I до точек класса II:

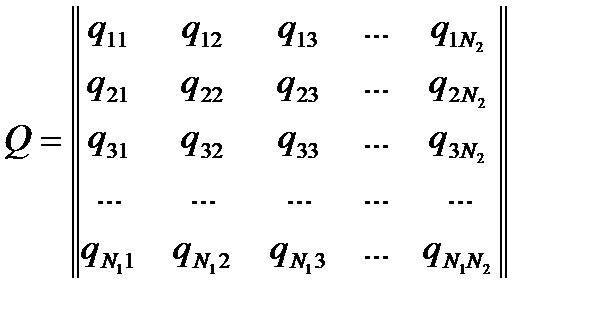
Формируются матрицы расстояний QQ и RR. Матрица не зависит от порядка расположения соединений. Так же, получаемые матрицы обладают одинаковой размерностью (N_i x N_i) и их можно вычитать друг из друга.

Определяют матрицу функционала:

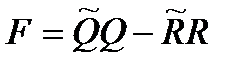
Результатом этой операции так же будет матрица размером N_i x N_i.

Требуется, чтобы F à max. Значит, нужно найти собственные векторы пространства, отвечающие за максимальные векторы матрицы F. Решают уравнение: FA = ΛA, где A – матрица собственных векторов, Λ – матрица собственных значений. Выбирают максимальное собственное значение и соответствующий ему собственный вектор:

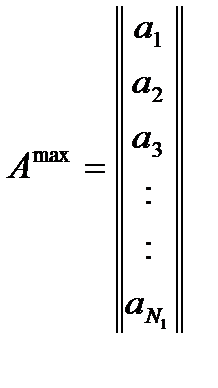
Элементами этого собственного вектора a_i являются информационные веса объектов. Информационные веса могут иметь отрицательные или положительные значения. Либо могут быть равны нулю.

a_i > 0 – объект вносит значительный вклад в образ класса;

a_i → 0 – объект не влияет на образ класса;

a_i < 0 – объект не входит в данный класс, либо является исключением.

Таким образом, с помощью этих информационных весов происходит автоматический учет выпадающих точек.

Определяется суммарное расстояние от каждой точки 1-го класса до новой точки (х):

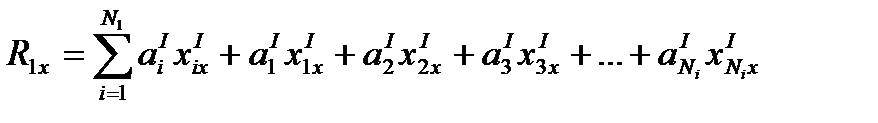
То же самое относительно точек 2-го класса:

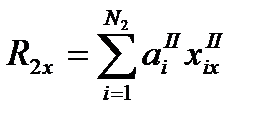
Если R_2x > R_1x, то точка относится к 1-му классу.

Получается, что [r₁r₂] ≠ [r₂r₁], т.е. на границе классов возникает неевклидово («катастрофическое») пространство.

Данный метод можно дополнительно «усилить» путем введения информационных весов факторов. Для этого формируют матрицу RR, элементами которой являются суммы расстояний между всеми точками одного класса по каждому фактору:

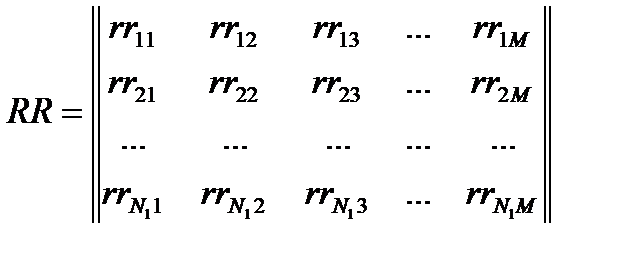
Затем формируют матицу QQ, элементами которой являются суммы расстояний от точек одного класса до точек другого класса по каждому фактору:

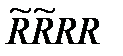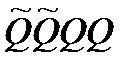Далее формируют информационные матрицы и , определяют матрицу функционала: .

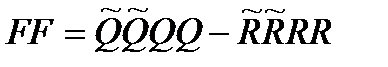Находят собственные векторы и собственные значения матрицы FF путем решения векового уравнения:

FFB=ΛB, где

В – матрица собственных векторов,

Λ – матрица собственных значений.

Находят максимальное собственное значение матрицы Λ, и соответствующий ему собственный вектор. Элементами этого собственного вектора будут информационные веса факторов для 1-го класса.

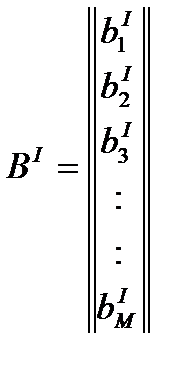
Аналогичную процедуру поводят и для 2-го класса.

Теперь для расчета расстояний между точками используют не простую евклидову близость, а следующее выражение:

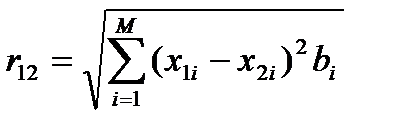
Такое пространство носит название диссипативного. Теперь для отнесения точек по классам необходимо рассчитывать расстояния до точек разных классов с учетом весов факторов. Таким образом учитывается не только важность каждой точки, но и значимость факторов.

Алгоритм «идеального эталона»: В каждом классе изначально выбираются по 2 точки: одна в центре класса, вторая – случайным образом. Для этих четырёх эталонных объектов решают задачу распознавания в рамках метода главных компонент, получают решающее правило. Проверяют его на всех имеющихся точках. Варьируют расположение эталонов с целью достижения максимума качества распознавания. Если получаемое качество не устраивает, можно добавить в каждый класс третий эталон. Т.о. идеальным эталоном называется минимальное количество обучающих объектов, обеспечивающее максимальное качество распознавания.