Метод Якоби ( метод простой итерации )

Рассмотрим систему линейных уравнений (2.1). Пусть 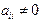. Это позволяет выразить 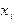в каждом из уравнений и привести исходную систему уравнений к виду:

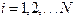, где . (2.4)

Такую систему можно решить методом Якоби (методом простой итерации), строя последовательность приближений по следующему правилу:

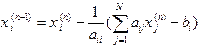, где 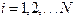; 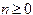. (2.5)

Идея решения системы (2.4) таким способом, очевидно, та же самая, что и для решения уравнений методом простой итерации с помощью формулы (1.6). По этой причине такой подход можно применять и для решения систем нелинейных уравнений. При решении систем уравнений итерационная последовательность представляет собой последовательность не чисел, а векторов N-мерного пространства. Очевидно, что и здесь эта последовательность может быть сходящейся или расходящейся. Этот вопрос решается на основании следующей теоремы о достаточном условии сходимости:

Если 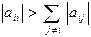для 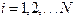, (2.6)

то итерационная последовательность (2.5) сходится к решению системы (2.1) при любом начальном приближении.

Другими словами, матрица коэффициентов исходной системы уравнений должна быть матрицей с диагональным преобладанием.

Пример. Рассмотрим систему трех уравнений с тремя неизвестными и найдем ее решение методом Якоби, оставляя каждый раз при вычислениях два знака после запятой:

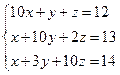; преобразуем эту систему к виду (2.4)

Возьмем в качестве начального приближения 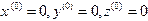. Тогда

, , , ...

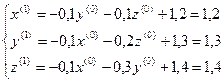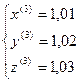Исходная система уравнений удовлетворяет условию (2.6), поэтому построенная последовательность будет сходиться к истинному решению системы ( 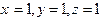). Вычисления можно прекратить, когда достигнем значения n такого, что .

Метод Зейделя

Другой итерационный способ решения систем линейных уравнений вида (2.4) носит имя Зейделя, и его можно рассматривать как модификацию метода Якоби. Последовательные приближения строятся здесь по формуле

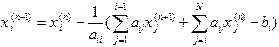, где 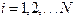; 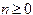. (2.7)

Отличия двух методов хорошо иллюстрирует следующий пример:

Пример. Рассматривая систему трех уравнений с тремя неизвестными, которая приводилась выше, найдем ее решение методом Зейделя, оставляя каждый раз при вычислениях два знака после запятой:

Возьмем в качестве начального приближения 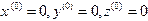. Тогда

, , , ...

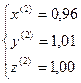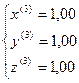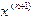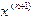Обратите внимание, что в методе Зейделя при вычислении используется уже найденное на этом шаге , а при вычислении используются и .

Приведенное решение показывает, что метод Зейделя быстрее сходится к решению, чем метод Якоби, однако в общем случае это неверно. Дело в том, что эти методы ориентированы на решение разных классов систем: метод Якоби - на системы с матрицами, близкими к диагональным, а метод Зейделя - на системы с матрицами, близкими к нижним треугольным.

Достаточные условия сходимости метода Зейделя формулируются следующей теоремой:

Если 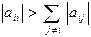для 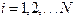, (2.8)

причем хотя бы для одного 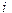неравенство строгое, то итерационная последовательность (2.7) сходится к решению системы (2.1) при любом начальном приближении.

Докажем эту теорему для системы двух уравнений с двумя неизвестными: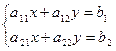

Пусть 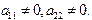Приведем эту систему к виду, удобному для итераций: , тогда . Подставляя 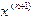из первого уравнения во второе, получим:

(*)

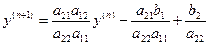для предыдущего шага итерации эта формула имеет вид

(**) Вычтем (**) из (*) и возьмем разность по абсолютной величине: . Аналогично можно получить, что
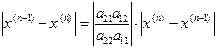. Известно, что итерационная схема сходится, если при . Это означает, что при выполнении условий теоремы и схема сходится, что и требовалось доказать.