АЛГЕБРАИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛОГИЧЕСКИХ ФУНКЦИЙ
Мы уже знаем, что логическая функция может быть представлена:
а) словесно: если Х1=1 и X2=1, то Y=1;
б) таблично: в виде таблицы истинности, которая содержит n+m столбцов и 2n строк (n-число входов или аргументов, m-число выходов);
| i | X1 | X2 | Y |
в) с помощью карт Карно (или диаграмм Вейча), которые представляют собой разновидность табличной формы задания логической функции;
г) числовым способом: когда функция задается в виде набора (множества) десятичных чисел, соответствующих номерам набора аргументов, при которых функция принимает значение 1;
Например, функция ИЛИ для аргументов Х1, Х2;
| Y | X1 | X2 |
Y={1,2,3}X1X2.
=0 Переменные указывают порядок
=1 формирования битов двоичного числа.
=2
=3 Для логической функции И Y={3}X1X2;
д) аналитически: в виде алгебраического выражения.
Рассмотрим более подробно алгебраическое представление логической функции.
Введем понятие терма. Термом обозначим функцию:
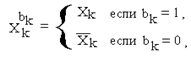
|
где: к = 0,1, ...,n ,
bk - константа 0 или 1.
При любом фиксированном значении переменной Xk=ak справедлива формула:
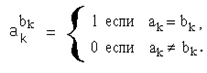
|
_
Действительно: 00=0=1; 11=1;
_
01=0 ; 10= 1=0.
Используя введенное обозначение, запишем функцию И (конъюнкцию) n логических переменных:
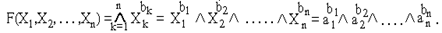
Эта функция принимает значение 1 только при одном наборе значений переменных (а1,а2, ...,аn), для которого выполняется условие ak=bk, для всех остальных наборов функция принимает значение 0.
Например: __ __
F(X1,X2, ...,X5)=X1×X2×X3×X4×X5=X01×X12×X03×X14×X15
принимает значение 1 только при одном наборе переменных (0,1,0,1,1).
Конъюнкция, в которую входят все переменные (аргументы логической функции) в прямой или инверсной форме, называется минтермом.
Минтерм обозначим C1i , где i-номер единственного набора, на котором C1i=1 (пример выше: 010112=1110 , следовательно - C111).
Алгебраически минтерм представляют в виде конъюнкции, в которую в прямой форме входят все переменные, имеющие в данном наборе значение 1, и в инверсной форме все переменные, имеющие в данном наборе значение 0.
Для логической функции двух переменных можно составить следующие минтермы:
| i | X1 | X2 | __ __ C10=X1×X2 | __ C11=X1×X2 | __ C12=X1×X2 | C13=X1×X2 |
Аналогично можно рассмотреть функцию ИЛИ (дизъюнкцию) n логических переменных:
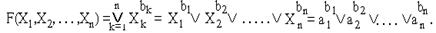
Логическая функция ИЛИ принимает значение F(×)=1, если хотя бы одна переменная Хbii=1. Следовательно, существует только один набор значений переменных, для которых выполняется условие ak ¹ bk , при котором функция принимает значение 0.
Например, функция: __ __
F(X1,X2,X3,X4,X5)=X1ÚX2ÚX3ÚX4ÚX5=X11ÚX12ÚX13ÚX04ÚX05
принимает значение 0 только при одном наборе (0,0,0,1,1).
Дизъюнкцию, в которую входят все переменные в прямой или инверсной форме, называютмакстермом.
Макстерм имеет обозначение C0i , где i-номер единственного набора, при котором C0i=0.
Рассмотренный выше пример: 000112 = 310 , следовательно - C03 .
Рассмотрим макстермы двух переменных:
| i | X1 | X2 | C00=X1Ú X2 | __ C01=X1ÚX2 | __ C02=X1ÚX2 | __ __ C03=X1ÚX2 |
Макстерм представляется в виде дизъюнкции, в которую в прямой форме входят все переменные, имеющие на данном наборе (при котором C0i=0) нулевые значения, и в инверсной форме - все переменные, имеющие на данном наборе значение 1.
Аналогично функциям И, ИЛИ можно ввести функцию И-НЕ для n переменных:
_____ ____________________ ________________
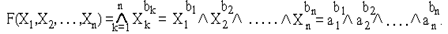
Эта функция, являясь инверсией конъюнкции n переменных, принимает значение 0 только на одном наборе переменных, для которого ak=bk . Для всех остальных наборов эта функция равна 1.
И, наконец, можно определить функцию ИЛИ-НЕ:
_____ ___________________ ________________
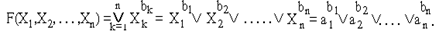
Эта функция принимает значение 1 только на одном наборе значений переменных, для которого ak¹bk , на всех остальных наборах эта функция равна 0.
Дата добавления: 2022-02-05; просмотров: 956;











