Дифференциальные тензоры
Составим диадное произведение вектора набла  и какого-нибудь переменного вектора, например
и какого-нибудь переменного вектора, например  .
.
Помня, что умножить на составляющую символического вектора  - это значит продифференцировать по соответствующей координате, находим:
- это значит продифференцировать по соответствующей координате, находим:
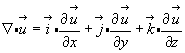 (3.44)
(3.44)
Этот тензор по аналогии с градиентом скалярной величины (см. формулу 3.33) назовем градиентом вектора:
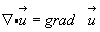 (3.42)
(3.42)
Его составляющие легко выявляются, если рассмотреть диадные произведения ортов на скалярные производные от вектора  в равенстве (3.41), и записываются в виде матрицы:
в равенстве (3.41), и записываются в виде матрицы:
Примечание:
Свойство сопряженного тензора:
Величина произведения вектора на тензор, не изменится, если при перестановке сомножителей тензор заменить на сопряженный.
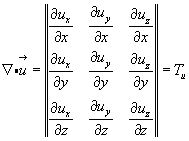 (3.43)
(3.43)
Умножим тензор grad  на дифференциал радиус вектора слева:
на дифференциал радиус вектора слева:
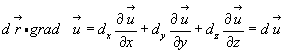 (3.44)
(3.44)
Полученное соотношение совершенно аналогично (3.37) полному дифференциалу скалярной функции. Т.е. имеем:
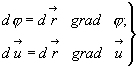 (3.44а)
(3.44а)
Если в тензоре (3.43) заменить элементы строк на элементы столбцов, то получим сопряженный тензор:
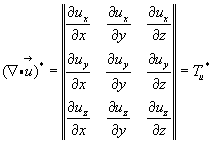 (3.45)
(3.45)
Если в другой записи (с учетом (3.6) и (3.7)):
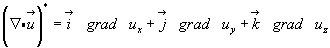 (3.46)
(3.46)
но по свойству сопряженного тензора равенство (3.44а) можно переписать в следующем виде:
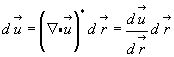 (3.47)
(3.47)
Следовательно, тензор (  ∙
∙  )* можно рассматривать как производную от векторной функции
)* можно рассматривать как производную от векторной функции  по векторному аргументу
по векторному аргументу 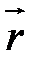 .
.
Дата добавления: 2019-12-09; просмотров: 760;











