Примеры, имеющие самостоятельное значение

1. Положение точки или частицы жидкости в декартовой системе координат характеризуется радиус-вектором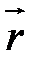

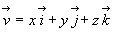
С помощью этого вектора распределене скоростей в пространстве дается соотношением 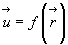, что эквивалентно трем скалярным уравнениям:

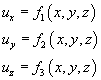
Приращение вектора 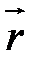- величина d 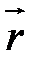(расстояние между двумя близкими точками) определяется равенством:

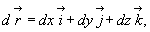
а скорость движения некоторой частицы представляется очевидным соотношением

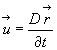
где D – символ субстационарной производной.

Умножим элементарный вектор d 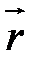на градиент некоторой скалярной функции φ:

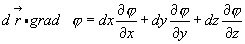
Замечаем, что правая часть этого равенства представляет собой полный дифференциал скалярной функции φ.

Т.о. имеем важную формулу:

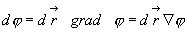(3.37)

2. Составим скалярное произведение единичного вектора 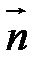и grad φ:

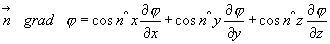
(здесь единичный вектор 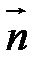в проекциях на оси координат представляется равенством:

)

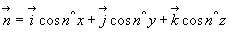Найдем производную от φ по направлению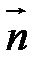

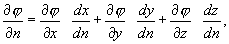
т.к.

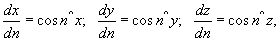
то

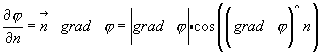
Замечание:

Из формулы (3.38) видно, что производная 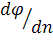достигает своего наибольшего значения для направления 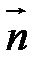, совпадающего с направлением grad φ, при этом ее наибольшее значение равно величине grad φ. Поэтому градиент скалярной функции можем определять как вектор, имеющий направление быстрейшего роста скалярной величины φ и равный производной от нее по этому направлению.

Именно поэтому, например, результирующая сила давления равна – grad P, т.к. она должна быть направлена в сторону быстрейшего падения давления, а результирующий тепловой поток – в сторону наибольшего уменьшения температуры, т.е. в сторону – grad T, как это следует из закона Фурье.

Замечание к разделу:

Координатное представление вектора набла позволяет во многих случаях упрощать формулы, записанные в символическом виде, и, таким образом, является существенным дополнением к нему.

Пример:

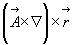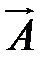Найдем выражение для , где - постоянный вектор:

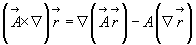
Далее, из соотношений сделанных при выводе формулы (3.28), получаем

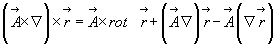
В этом выражении последующие преобразования невозможны.

Но, если обратиться к координатному представлению рассмотренных нами операций, сразу замечаем, что величина 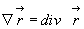оказывается равной

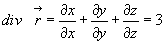
т.о.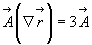

rot 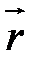= 0, т.к. производные от одних независимых переменных по другим тождественно равны нулю (см. 3.34).

Кроме того:

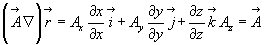
т.о. получим простое соотношение:

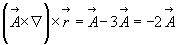
Казалось бы, что этот пример наталкивает на мысль, что символический метод совершенно не нужен, т.к. непосредственным вычислением в координатном представлении можно получить все необходимые преобразования.

Это действительно так, однако если попытаться вывести такие простые зависимости, как:

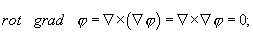
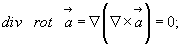
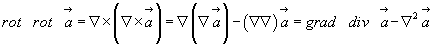
опираясь лишь на координатное выражение оператора Гамильтона, можно сразу оценить существенную экономию труда и бумаги, а также элегантность операций, которые сопутствуют символическому методу исчисления.