Дифференциальные зависимости при прямом поперечном изгибе
Построение эпюр поперечных сил и изгибающих моментов существенно упрощается при использовании дифференциальных зависимостей между изгибающим моментом, поперечной силой и интенсивностью равномерно распределенной нагрузки (теорема Журавского):
Поперечная сила равна производной от изгибающего момента по длине балки:
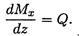
Интенсивность равномерно распределенной нагрузки равна производной от поперечной силы по длине балки:
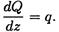
Из выше указанного следует:

Контрольные вопросы
1. Какую плоскость называют силовой?
2. Какой изгиб называют прямым? Что такое косой изгиб?
3. Какие силовые факторы возникают в сечении балки при чистом изгибе?
4. Какие силовые факторы возникают в сечении при поперечном изгибе?
 |
5. Определите поперечную силу и изгибающий момент в сечении 1-1 (рис. 29.7). Расстояние сечения от свободного конца балки 5 м.
6. Определите реакцию в опоре В.
7. Определите величину поперечной силы и изгибающего момента в сечении С, использовав схему балки (рис. 29.8).
8. Определите участок чистого изгиба (рис. 29.9).

ЛЕКЦИЯ 30
Дата добавления: 2020-08-31; просмотров: 652;











