Представление дифференциальных операций векторного анализа в декартовой системе координат

Декартова система координат является наиболее распространенной для описания движения жидкости в трехмерном пространстве.

Рассмотрим представление всех рассмотренных понятий и операций в декартовой системе координат, обращая главное внимание лишь на физическое содержание векторных операций и правила их использования и не ставя перед собой задачу строгого доказательства тех или иных положений.

С учетом этого сразу можем написать

1. 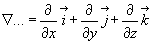(3.31)

Таким образом, проекции вектора набла на оси прямоугольной декартовой системы координат есть операторы (производные) 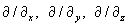. Поэтому умножить проекцию вектора набла

Примечание:

5. скалярные операторы ²…

6. ( )…

будучи примененными к скалярной функции 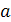, дадут зависимости:

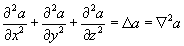
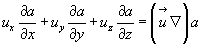
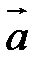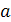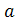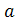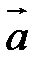Если есть вектор, то, представляя его тремя скалярными функциями _x; _y; _z (проекции на оси координат) для ² и ( ) 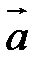получим по три формулы, аналогичные приведенным (выше).

Например:

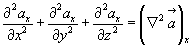
на проекцию какого-либо другого вектора – это значит продифференцировать ее по соответствующей координате.

Учитывая это и применяя правило действия над векторами, получаем:

2. 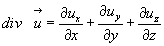(3.32)

3. 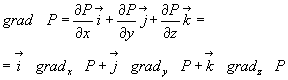(3.33)

4. 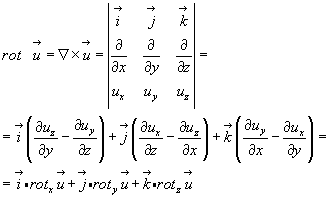(3.34)

5. 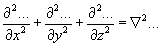(3.35)

6. 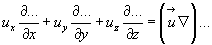(3.36)