Оператор Лапласса (лапласиан)

Наряду с дифференциальными операциями первого порядка в векторном анализе находят частое применение также дифференциальные операции второго порядка. Такой операцией и является лапласиан от некоторой скалярной или векторной функции.

Оператор … или ² … называемый оператором Лапласса, формально может быть получен как скалярное произведение вектора набла на вектор набла:

…

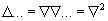Таким образом применение знака (символа) ² … или … к какой-либо скалярной или векторной величине можно трактовать как двойное ее дифференцирование по трем пространственным координатам, т.е. по объему.

В векторном анализе показывается, что математически лапласиан определяется соотношением:

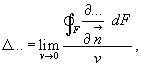(3.30)

которое вскрывает и смысл этой операции.

Действительно, под знаком интеграла стоит производная по направлению 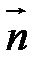, нормальному к элементарной площадке dF, от некоторой физической характеристики.

Если эта характеристика по всем направлениям от поверхности, охватывающей данный объем, растет, то сам интеграл оказывается положительным и тогда значение самой характеристики внутри объема меньше, чем в его окрестностях. Если же значение характеристики убывает в направлении нормалей от поверхности, то внутри объема сама характеристика больше, чем в окружающем ее пространстве. Интеграл в этом случае будет иметь отрицательное значение. В общем случае он может иметь и тот, и другой знак быть равным нулю.

Таким образом, лапласиан представляет собой отклонение некоторой физической характеристики внутри бесконечно малого объема от среднего значения той же характеристики в окрестностях этого объема.

Вычисляя лапласиан некоторой величины, мы тем самым определяем величину, указанного отклонения.

В гидродинамике большое значение имеет лапласиан скорости т.е. ² , а в теории теплопроводности огромную роль играет лапласиан температуры ² .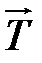

Замечание:

Опираясь на приведенные разъяснения, можно придти к выводу, что касательные вязкие силы, действующие в жидкости, должны быть, по-видимому, пропорциональны лапласиану скорости, т.к. трение малого объема о соседние частицы той же среды, очевидно будет тем больше, чем больше скорость его отличается от средней скорости этих частиц.

Примеры:

1.

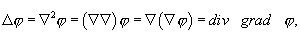
где φ – скалярная функция.

Примечание: По правилам векторной алгебры безразлично, умножается ли вектор сам на себя вначале, а затем уже на скаляр, или берется скалярное произведение вектора на другой вектор, умноженный на скаляр.

2.

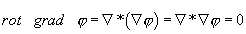
3.

4.

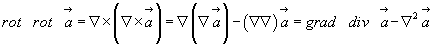
Важное замечание:

Все введенные понятия рассматривались безотносительно к какой-либо системе координат и, следовательно, верны в любой системе отсчета. В этом заключается их большая универсальность. Однако представленный (рассмотренный) символический метод не всемогущ. Он удобен при выводе и преобразованиях основных дифференциальных уравнений, для выявления их физического содержания.

Однако, как только возникает необходимость решения этих уравнений, приходится прибегать к представлению векторов через скалярные функции, т.е. обращаться к их проекциям на оси той или иной системы координат.