Безвихревые и соленоидальные векторные поля

Будем считать, что в некоторой области V задано векторное поле, если в каждой точке М 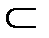V определен вектор

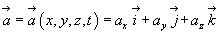
В гидродинамике важную роль играют векторные поля, удовлетворяющие во всех точках области определения условиям:

1) 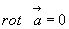(3.48)

2) 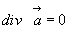(3.49)

В первом случае (т.е. при rot 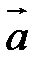= 0) поле называется безвихревым, а во втором (т.е. при div 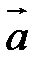= 0) – соленоидным.

Справедлива теорема:

Для того чтобы поле вектора 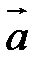было безвихревым, необходимо и достаточно существование такой скалярной функции 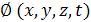, называемой потенциалом векторного поля, для которой во всех точках области задания векторного поля выполнялось бы равенство

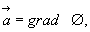(3.50)

причем функция 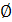вместе с частными производными первого и второго порядка непрерывна в рассматриваемой области.

Следствие:

Выражения «безвихревое поле» и «потенциальное поле» являются синонимами, т.е. для задания векторного поля достаточно задать скалярное поле потенциала.

Пример:

Потенциальным векторным полем является напряженности гравитационных сил вблизи поверхности Земли.

В этом случае проекции силы тяжести, действующей на единицу массы, определяется выражениями:

F_x = 0; F_y = 0; F_z = -g

Следовательно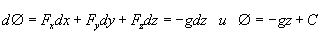

Отсюда видно, что в данном случае потенциал 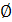численно равен величине потенциальной энергии единицы массы, взятой со знаком минус. Именно это обстоятельство объясняет происхождение термина «потенциал».

Замечание:

Если безвихревое (или потенциальное) поле одновременно является соленоидальным, то лапласиан его потенциала равен нулю

т.е. Δ 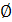= 0