ДИФФЕРЕНЦИАЛЬНЫЕ КРИТЕРИИ
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
Множество  называется выпуклым, если с любыми двумя точками
называется выпуклым, если с любыми двумя точками 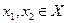 оно содержит отрезок, их соединяющий. Иначе это определение можно сформулировать так: множество
оно содержит отрезок, их соединяющий. Иначе это определение можно сформулировать так: множество  выпукло, если
выпукло, если 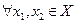 точка
точка 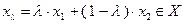 при всех
при всех 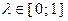 . На рис. 3.1.1 представлена геометрическая иллюстрация выпуклого и невыпуклого множеств.
. На рис. 3.1.1 представлена геометрическая иллюстрация выпуклого и невыпуклого множеств.
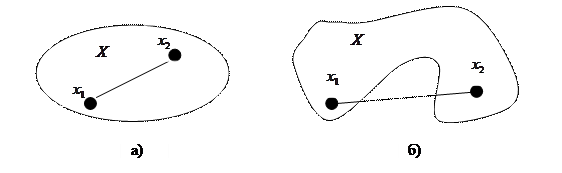
Рис. 3.1.1. Геометрическая иллюстрация выпуклого (а) и невыпуклого (б) множеств
Пространство 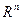 образует выпуклое множество. Пустое множество и множество, состоящее из одной точки, удобно считать выпуклыми. Тогда из определения выпуклого множества следует, что пересечение любого числа выпуклых множеств является выпуклым множеством.
образует выпуклое множество. Пустое множество и множество, состоящее из одной точки, удобно считать выпуклыми. Тогда из определения выпуклого множества следует, что пересечение любого числа выпуклых множеств является выпуклым множеством.
Функция  , определенная на выпуклом множестве
, определенная на выпуклом множестве  , называется выпуклой на этом множестве, если
, называется выпуклой на этом множестве, если 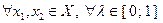 выполнено неравенство
выполнено неравенство
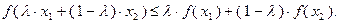 (3.1.1)
(3.1.1)
На рис. 3.1.2 в качестве примера приведен график выпуклой функции одной переменной 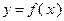 . Выпуклую функцию можно определить как функцию,
. Выпуклую функцию можно определить как функцию,
|

Рис. 3.1.2. Пример выпуклой функции одной переменной
над графиком которой – выпуклое множество.
Функция  называется вогнутой на выпуклом множестве
называется вогнутой на выпуклом множестве  , если функция
, если функция 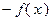 выпукла на
выпукла на  . Вогнутую функцию можно определить также как функцию, под графиком которой – выпуклое множество.
. Вогнутую функцию можно определить также как функцию, под графиком которой – выпуклое множество.
Существуют подклассы выпуклых функций. Так, функция  , определенная на выпуклом множестве
, определенная на выпуклом множестве  , называется строго выпуклой на
, называется строго выпуклой на  , если
, если 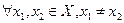 и
и 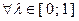 равенство в (3.1.1) имеет место только при
равенство в (3.1.1) имеет место только при 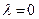 и
и 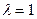 .
.
Функция  называется строго вогнутой на выпуклом множестве
называется строго вогнутой на выпуклом множестве  , если функция
, если функция 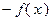 строго выпукла на
строго выпукла на  .
.
Например, функция одной переменной 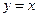 является одновременно выпуклой и вогнутой на
является одновременно выпуклой и вогнутой на 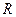 , однако не является ни строго выпуклой, ни строго вогнутой.
, однако не является ни строго выпуклой, ни строго вогнутой.
Функция  , определенная на выпуклом множестве
, определенная на выпуклом множестве  , называется сильно выпуклой (сильно выпуклой с константой
, называется сильно выпуклой (сильно выпуклой с константой 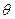 ) на
) на  , если
, если 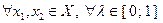 выполнено неравенство
выполнено неравенство
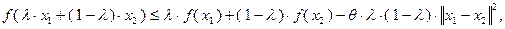 (3.1.2)
(3.1.2)
где 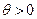 ,
, 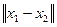 – евклидова норма (длина вектора):
– евклидова норма (длина вектора):
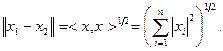 (3.1.3)
(3.1.3)
Функция  , определенная на выпуклом множестве
, определенная на выпуклом множестве  , называется сильно вогнутой на этом множестве, если функция
, называется сильно вогнутой на этом множестве, если функция 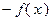 сильно выпукла на
сильно выпукла на  .
.
Функция, сильно выпуклая на множестве  , является выпуклой и строго выпуклой на этом множестве.
, является выпуклой и строго выпуклой на этом множестве.
Пример 3.1.1. Показать, что функция одной переменной 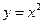 сильно выпукла на
сильно выпукла на 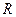 .
.
Левая часть неравенства (3.1.2) в данном случае принимает вид:
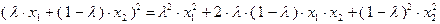 . (3.1.4)
. (3.1.4)
Вычитая выражение (3.1.4) из первых двух слагаемых правой части неравенства (3.1.2), получим:
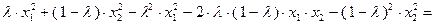
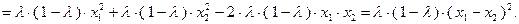
Таким образом, неравенство (3.1.2) превращается в тождественное равенство при 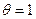 и, следовательно, функция
и, следовательно, функция 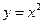 является сильно выпуклой на
является сильно выпуклой на 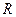 с константой
с константой 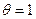 .
.
В практических задачах важное значение имеет выяснение наличия у исследуемых функций свойств выпуклых функций, либо их отсутствия.
Рассмотрим некоторые теоремы, которые могут быть использованы для проверки выпуклости функций.
Теорема 3.1.1
Пусть функции 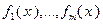 – выпуклы на множестве
– выпуклы на множестве  и числа
и числа 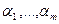 неотрицательны. Тогда функция
неотрицательны. Тогда функция
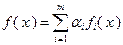
выпукла на множестве  . Читателю предлагается доказать эту теорему самостоятельно.
. Читателю предлагается доказать эту теорему самостоятельно.
Теорема 3.1.2
Дана функция 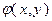 , обладающая следующими свойствами:
, обладающая следующими свойствами:
1) функция 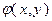 определена на множестве
определена на множестве 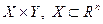 ,
,  – выпуклое множество;
– выпуклое множество;
2) функция 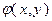 выпукла по
выпукла по 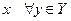 ;
;
3) функция 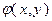 ограничена сверху по
ограничена сверху по 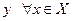 .
.
Тогда функция 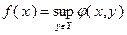 выпукла на множестве
выпукла на множестве  .
.
Доказательство. Для любых точек 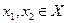 и для любого
и для любого 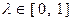 можно записать:
можно записать:
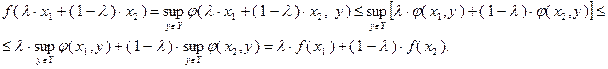
Таким образом, неравенство (3.1.1) выполнено, и, следовательно, теорема доказана.
В случае 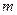 функций одной переменной
функций одной переменной 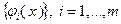 , рассматривая индекс
, рассматривая индекс 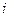 в качестве аналога переменной
в качестве аналога переменной 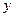 из теоремы 3.1.2, завершающую часть формулировки этой теоремы можно записать в виде заключения о выпуклости функции
из теоремы 3.1.2, завершающую часть формулировки этой теоремы можно записать в виде заключения о выпуклости функции
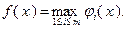
На рис. 3.1.3 представлены графики двух выпуклых функций одной переменной 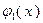 и
и 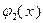 . График, показанный сплошной линией, является графиком функции
. График, показанный сплошной линией, является графиком функции
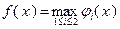 ,
,
которая согласно теореме 3.1.2 является выпуклой.
Теорема 3.1.3
Пусть функция 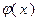 выпукла на выпуклом множестве
выпукла на выпуклом множестве 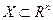 , а функция
, а функция 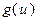 выпукла и монотонно не убывает на выпуклом множестве
выпукла и монотонно не убывает на выпуклом множестве 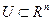 , причем
, причем 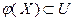 . Тогда функция
. Тогда функция 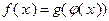 выпукла на множестве
выпукла на множестве  .
.
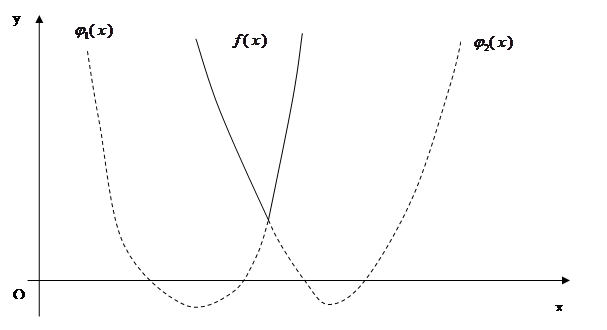
Рис. 3.1.3. Пример применения теоремы 3.1.2 для случая двух функций одной переменной
Доказательство. 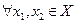 и
и 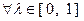 можно записать:
можно записать:
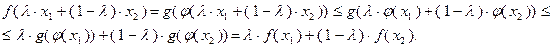 (3.1.5)
(3.1.5)
Первое из приведенных неравенств справедливо на том основании, что, во-первых,
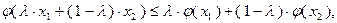
так как функция 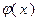 выпукла, и, во-вторых, что функция
выпукла, и, во-вторых, что функция 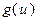 монотонно не убывает. Справедливость второго неравенства в (3.1.5) объясняется выпуклостью функции
монотонно не убывает. Справедливость второго неравенства в (3.1.5) объясняется выпуклостью функции 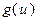 . Теорема доказана.
. Теорема доказана.
Применение рассмотренных теорем к решению практических задач продемонстрируем на следующем примере.
Пример 3.1.2. Выяснить, является ли выпуклой функция
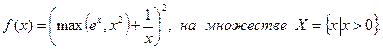
Функция 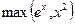 является выпуклой по теореме 3.1.2. Функция
является выпуклой по теореме 3.1.2. Функция 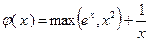 выпукла в соответствии с теоремой 3.1.1. Наконец, функция
выпукла в соответствии с теоремой 3.1.1. Наконец, функция 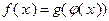 , где
, где 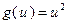 , является выпуклой по теореме 3.1.3. Таким обрзом, заданная в примере функция выпукла.
, является выпуклой по теореме 3.1.3. Таким обрзом, заданная в примере функция выпукла.
Следующую теорему читателю предлагается доказать самостоятельно.
Теорема 3.1.4
1. Пусть функция  является строго выпуклой на выпуклом множестве
является строго выпуклой на выпуклом множестве  . Тогда
. Тогда 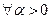 функция
функция 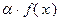 строго выпукла на
строго выпукла на  .
.
2. Пусть функция  является сильно выпуклой с константой
является сильно выпуклой с константой 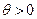 на выпуклом множестве
на выпуклом множестве  . Тогда
. Тогда 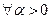 функция
функция 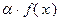 сильно выпукла с константой
сильно выпукла с константой 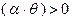 на
на  .
.
3. Пусть функция 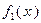 выпукла на выпуклом множестве
выпукла на выпуклом множестве  , а функция
, а функция 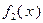 сильно выпукла с константой
сильно выпукла с константой 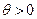 на
на  . Тогда функция
. Тогда функция 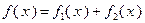 является сильно выпуклой с константой
является сильно выпуклой с константой 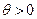 на
на  .
.
4. Пусть функция 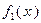 выпукла на выпуклом множестве
выпукла на выпуклом множестве  , а функция
, а функция 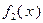 строго выпукла на
строго выпукла на  . Тогда функция
. Тогда функция 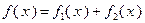 является строго выпуклой на
является строго выпуклой на  .
.
Заметим, что линейная функция 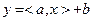 является одновременно выпуклой и вогнутой на выпуклом множестве
является одновременно выпуклой и вогнутой на выпуклом множестве  и что только линейные функции обладают таким свойством. При этом линейная функция не является ни строго выпуклой (вогнутой), ни сильно выпуклой (вогнутой). Всякая сильно выпуклая функция является строго выпуклой, но не наоборот. Например, функция
и что только линейные функции обладают таким свойством. При этом линейная функция не является ни строго выпуклой (вогнутой), ни сильно выпуклой (вогнутой). Всякая сильно выпуклая функция является строго выпуклой, но не наоборот. Например, функция 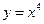 строго выпукла на
строго выпукла на 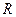 , но не является сильно выпуклой.
, но не является сильно выпуклой.
ДИФФЕРЕНЦИАЛЬНЫЕ КРИТЕРИИ
ВЫПУКЛОСТИ ФУНКЦИЙ
В тех случаях, когда рассматриваемая функция является дифференцируемой на заданном множестве, выяснение вопроса о ее выпуклости может быть осуществлено с помощью дифференциальных критериев выпуклости. Напомним, что функция дифференцируема в точке 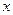 , если ее приращение в этой точке может быть записано в виде:
, если ее приращение в этой точке может быть записано в виде:
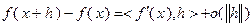 (3.2.1)
(3.2.1)
и дважды дифференцируема в точке 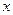 , если
, если
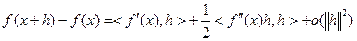 (3.2.2)
(3.2.2)
Теорема 3.2.1
Пусть функция  дифференцируема на открытом выпуклом множестве
дифференцируема на открытом выпуклом множестве  . В этом случае функция
. В этом случае функция  выпукла на
выпукла на  тогда и только тогда, когда
тогда и только тогда, когда 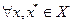 выполнено неравенство
выполнено неравенство
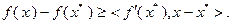 (3.2.3)
(3.2.3)
Доказательство. Пусть функция  выпукла на
выпукла на  , т.е.
, т.е. 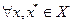 и
и 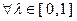 выполнено неравенство
выполнено неравенство
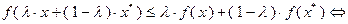
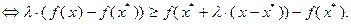 (3.2.4)
(3.2.4)
Из неравенства (3.2.4) следует:
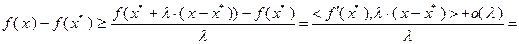
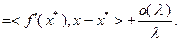
Поскольку 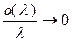 при
при 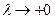 , неравенство (3.2.3) будет выполнено.
, неравенство (3.2.3) будет выполнено.
Теперь рассмотрим доказательство в обратную сторону. 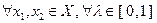 определим точку
определим точку 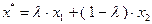 . Предположим, что выполнены неравенства:
. Предположим, что выполнены неравенства:
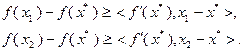
Умножив левую и правую части первого из этих неравенств на 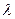 , второго – на
, второго – на 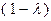 , затем сложив их, получим:
, затем сложив их, получим:
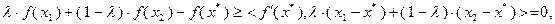
так как 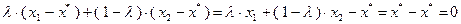 . Поэтому
. Поэтому
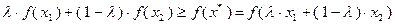 , т.е. функция
, т.е. функция  выпукла на множестве
выпукла на множестве  . Теорема доказана.
. Теорема доказана.
Доказанную теорему можно уточнить для случаев строгой и сильной выпуклости функции  . Приведем формулировки соответствующих теорем.
. Приведем формулировки соответствующих теорем.
Теорема 3.2.1а
Пусть функция  дифференцируема на открытом выпуклом множестве
дифференцируема на открытом выпуклом множестве  . В этом случае функция
. В этом случае функция  строго выпукла на
строго выпукла на  тогда и только тогда, когда
тогда и только тогда, когда 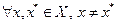 выполнено неравенство
выполнено неравенство
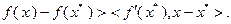
Теорема 3.2.1б
Пусть функция  дифференцируема на открытом выпуклом множестве
дифференцируема на открытом выпуклом множестве  . В этом случае функция
. В этом случае функция  сильно выпукла на
сильно выпукла на  с константой
с константой 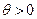 тогда и только тогда, когда
тогда и только тогда, когда 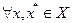 выполнено неравенство
выполнено неравенство
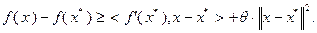
Выполнению условий теоремы 3.2.1 в одномерном случае соответствует расположение графика функции  при
при 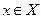 целиком выше касательной к нему, проведенной в любой точке с абсциссой, принадлежащей множеству
целиком выше касательной к нему, проведенной в любой точке с абсциссой, принадлежащей множеству  .
.
Дальнейшее изложение дифференциальных критериев выпуклости функций требует напоминания некоторых определений.
Квадратная матрица 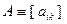 называется симметрической, если
называется симметрической, если 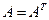 (
( 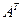 – транспонированная матрица), т.е. если
– транспонированная матрица), т.е. если 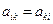 .
.
Вещественная симметрическая матрица 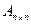 называется неотрицательно определенной (
называется неотрицательно определенной ( 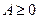 ), если
), если 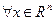 выполнено неравенство
выполнено неравенство 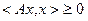 .
.
Вещественная симметрическая матрица 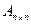 называется положительно определенной (
называется положительно определенной ( 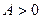 ), если
), если 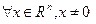 выполнено неравенство
выполнено неравенство 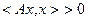 .
.
Вещественная симметрическая матрица 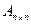 называется сильно положительно определенной, если
называется сильно положительно определенной, если 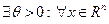 выполнено неравенство
выполнено неравенство 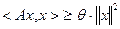 .
.
В соответствии с критерием Сильвестра вещественная симметрическая матрица является неотрицательно определенной тогда и только тогда, когда все ее главные миноры неотрицательны, и является положительно определенной тогда и только тогда, когда все ее угловые миноры положительны.
Определитель 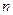 -го порядка
-го порядка 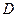 матрицы
матрицы 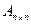 имеет
имеет 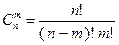 главных миноров
главных миноров 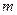 -го порядка, диагональные элементы которых являются и диагональными элементами
-го порядка, диагональные элементы которых являются и диагональными элементами 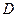 . Угловой минор
. Угловой минор 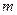 -го порядка – это главный минор, который состоит из элементов определителя
-го порядка – это главный минор, который состоит из элементов определителя 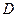 , находящихся одновременно в
, находящихся одновременно в 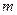 его первых строках и
его первых строках и 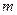 первых столбцах.
первых столбцах.
Например, матрица 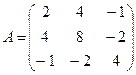 имеет следующие главные миноры:
имеет следующие главные миноры: 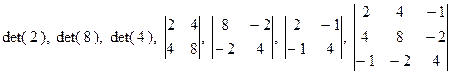 и следующие угловые миноры:
и следующие угловые миноры: 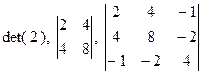 .
.
Теорема 3.2.2
Пусть функция  дважды непрерывно дифференцируема на открытом выпуклом множестве
дважды непрерывно дифференцируема на открытом выпуклом множестве 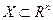 . В этом случае функция
. В этом случае функция  выпукла на
выпукла на  тогда и только тогда, когда
тогда и только тогда, когда 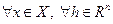 выполнено неравенство
выполнено неравенство 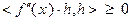 , т.е. матрица Гессе неотрицательно определена.
, т.е. матрица Гессе неотрицательно определена.
Доказательство. Пусть функция  выпукла на множестве
выпукла на множестве  . Выберем произвольно точку
. Выберем произвольно точку 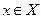 и
и 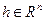 . В силу открытости множества
. В силу открытости множества  при достаточно малых значениях
при достаточно малых значениях 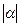 имеем
имеем 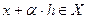 . В соответствии с (3.2.2) запишем:
. В соответствии с (3.2.2) запишем:
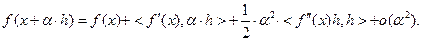 (3.2.5)
(3.2.5)
Из (3.2.5) и теоремы 3.2.1 следует:
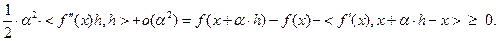
Поэтому
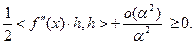
При 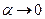 имеем
имеем 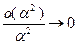 и, следовательно,
и, следовательно, 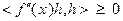 .
.
Теперь рассмотрим доказательство в обратную сторону. Пусть 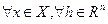 выполнено неравенство
выполнено неравенство 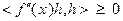 . Выберем произвольно точки
. Выберем произвольно точки 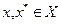 и введем обозначение:
и введем обозначение: 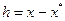 . Используя вариант формулы (3.2.2), соответствующий представлению остаточного члена формулы Тейлора в форме Лагранжа, запишем:
. Используя вариант формулы (3.2.2), соответствующий представлению остаточного члена формулы Тейлора в форме Лагранжа, запишем:
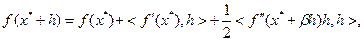 (3.2.6)
(3.2.6)
где 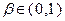 и
и 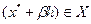 в силу выпуклости множества
в силу выпуклости множества  . Из выражения (3.2.6) следует:
. Из выражения (3.2.6) следует:
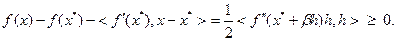
В соответствии с теоремой 3.2.1 функция  выпукла на
выпукла на  . Теорема доказана.
. Теорема доказана.
Для случаев строгой и сильной выпуклости функции  соответствующие теоремы формулируются следующим образом.
соответствующие теоремы формулируются следующим образом.
Теорема 3.2.2а
Пусть функция  дважды непрерывно дифференцируема на открытом выпуклом множестве
дважды непрерывно дифференцируема на открытом выпуклом множестве 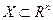 . В этом случае функция
. В этом случае функция  строго выпукла на
строго выпукла на  тогда и только тогда, когда
тогда и только тогда, когда 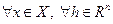 выполнено неравенство
выполнено неравенство 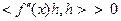 , т.е. матрица Гессе положительно определена.
, т.е. матрица Гессе положительно определена.
Теорема 3.2.2б
Пусть функция  дважды непрерывно дифференцируема на открытом выпуклом множестве
дважды непрерывно дифференцируема на открытом выпуклом множестве 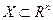 . В этом случае функция
. В этом случае функция  сильно выпукла на
сильно выпукла на  с константой
с константой 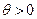 тогда и только тогда, когда
тогда и только тогда, когда 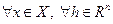 выполнено неравенство
выполнено неравенство 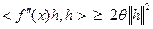 .
.
Например, для функции одной переменной 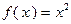 имеем:
имеем:
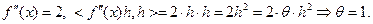
Таким образом, функция 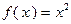 является сильно выпуклой на
является сильно выпуклой на 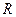 с константой
с константой 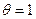 .
.
Пример 3.2.1. Является ли выпуклой функция
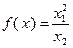 на множестве
на множестве 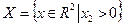 ?
?
Матрица Гессе для заданной функции имеет вид:
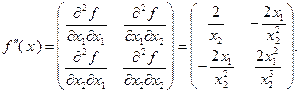
Чтобы выяснить, является ли полученная матрица Гессе неотрицательно определенной, воспользуемся критерием Сильвестра. Для этого найдем главные миноры определителя матрицы Гессе (называемого гессианом) и установим, все ли они неотрицательны. Рассматриваемая матрица имеет три главных минора:
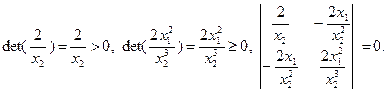
Поскольку все главные миноры неотрицательны, матрица Гессе неотрицательно определена, и в соответствии с теоремой 3.2.2 заданная функция  является выпуклой на
является выпуклой на  .
.
В случае, если функция  имеет вид
имеет вид
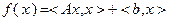 , (3.2.7)
, (3.2.7)
где 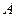 – симметрическая матрица, то
– симметрическая матрица, то  выпукла на
выпукла на 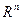 тогда и только тогда, когда матрица
тогда и только тогда, когда матрица 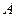 неотрицательно определена (
неотрицательно определена ( 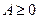 ) и сильно выпукла на
) и сильно выпукла на 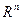 тогда и только тогда, когда матрица
тогда и только тогда, когда матрица 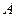 положительно определена (
положительно определена ( 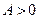 ). Это следует из того, что для функции (3.2.7)
). Это следует из того, что для функции (3.2.7) 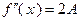 и из теорем 3.2.2, 3.2.2б.
и из теорем 3.2.2, 3.2.2б.
Помимо рассмотренных, существуют и другие способы выяснения выпуклости функций. Один из них связан с понятием множества Лебега. Если функция  определена на множестве
определена на множестве  , то множеством Лебега называется множество
, то множеством Лебега называется множество
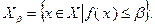
Соответствующая теорема формулируется следующим образом.
Теорема 3.2.3
Если функция  сильно выпукла на выпуклом множестве
сильно выпукла на выпуклом множестве  , то все ее множества Лебега на
, то все ее множества Лебега на  ограничены.
ограничены.
Рис. 3.2.1 иллюстрирует ограниченность множества Лебега 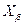 сильно выпуклой функции
сильно выпуклой функции  в одномерном случае.
в одномерном случае.
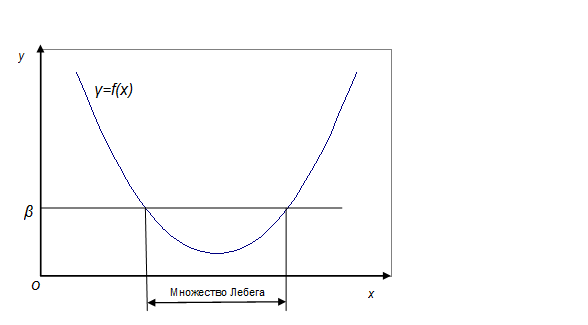
Рис. 3.2.1. Множество Лебега 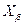 для функции
для функции 
Дата добавления: 2021-05-28; просмотров: 726;











