Кинематика жидкой частицы (движение жидкой частицы в общем виде)

Поставим перед собою такую задачу:

Пусть известна скорость жидкости 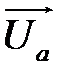в точке 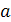, определенный радиус-вектором .

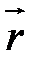Требуется найти скорость в некоторой другой точке, отстоящей от 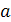на некоторое малое расстояние δ 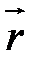. Как это сделать?

Применяя формально правила дифференциального исчисления, можно записать равенство

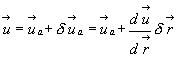(4.7)

Замечаем, что производная 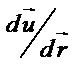представляет собой отношение двух бесконечно малых векторов 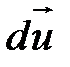и .

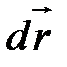Раньше мы договорились, что отношение двух векторов есть тензор, однако вследствие многозадачности операции деления векторов тензор пока неизвестен.

Отыскание этого тензора требует специальных рассуждений.

Раньше мы получили (см. формула 3.47), что тензор ( ∙ )* можно рассматривать как производную от векторной функции по векторному аргументу .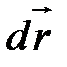

Рассмотрим более детально тензор ( ∙ )*, в котором под вектором будем понимать скорость. Для этого разложим тензор ( ∙ )* в соответствии с равенством (3.11) на симметричную и антисимметричную часть:

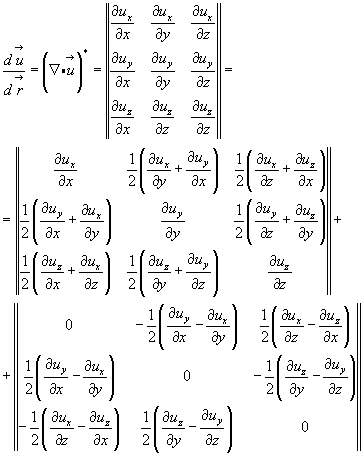(4.8)

Выясним, какую физическую трактовку можно дать этим двум составляющим тензорам.

Представим себе жидкую частицу в форме маленького кубика с гранями, параллельными осям координат.

В процессе движения такой частицы из-за слабости связей между ее элементами одни точки ее будут перемещаться быстрее, а другие медленнее, причем направления скоростей в разных точках, совсем не обязательно должны совпадать.

В результате рассматриваемая частица изменит свою форму и через некоторый промежуток времени δt приобретет вид, показанный на рисунке штриховой линией.

(Рассматриваем сечение этой частицы плоскостью ).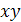

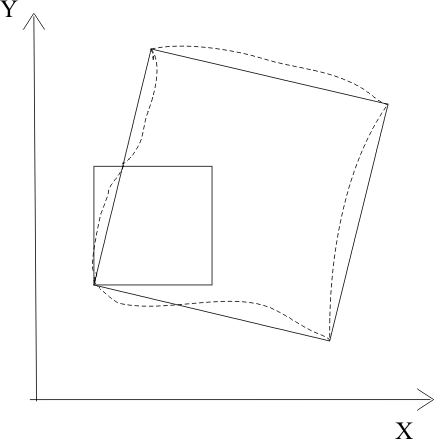
Рис. Сечение жидкой частицы плоскостью xy

Однако если первоначальные размеры частицы были очень малы, то кривые линии, очерчивающие новые контуры частицы, можно с точностью до бесконечно малых высших порядков заменить прямыми, как это обычно делается в дифференциальном исчислении.

Рассмотрим, какие превращения должны были бы произойти с элементарным кубиком, чтобы он превратился в частицу другой формы и, вообще говоря, по-новому ориентированную в пространстве.

Чтобы не осложнять рассуждений, будем рассматривать сечение частицы плоскостью .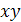

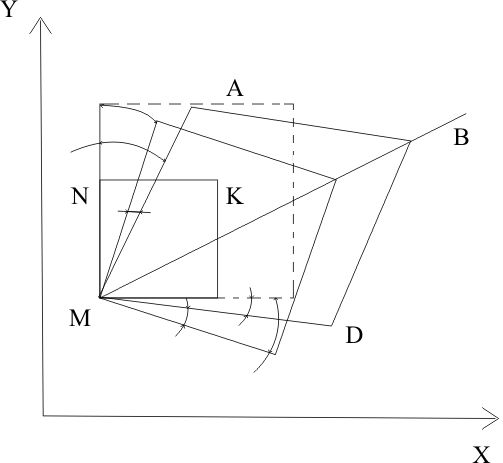
Нарисуем частицу в более крупном масштабе, дополнив схему вспомогательными линиями и обозначениями.

Примечание:

Такой подход к деформации частицы основывается на переносе уже известных представлений из механики и сопротивления материалов в гидродинамику и распространении их на движение жидкой частицы.

Такой подход очень распространен в науке. Нужно лишь удостовериться в правильности выбранной гипотезы.

L

δj

δα

δj

δθ

δβ

δθ

Вообразим, что первоначальный контур частицы MNKL за интервал времени δt перешел в контур MABD путем трех последовательных превращений.

1. Вначале частица растянулась или сжалась вдоль осей .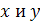

2. Затем она повернулась как единое целое на угол δγ.

3. Затем произошел ее сдвиг (сплющивание) на удвоенный угол δθ.

Замечание: выбор таких трех последовательных превращений частицы условен. Никаких оснований для этого нет, т.е. мы выдвигаем гипотезу, что растяжение, поворот и сдвиг деформируют частицу и т.о. переводят контур MNKL в контур MABD.

Такое расчленение движения удобно потому, что трудно уследить сразу за всеми изменениями, происходящими с частицей, которые в действительности протекают одновременно.

Возьмем любую точку внутри исходной частицы с координатами 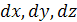по отношению к точке М.

Примечание:

эта скорость обусловлена растяжением или сжатием элементарной частицы по направлению оси .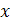

Посмотрим, какой величине будет пропорциональна скорость удаления этой точки от точки M в направлении оси x вследствие расширения или сжатия частицы.

Если скорость в точке M принять равной 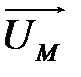, то смещение выбранной (рассматриваемой) точки по отношению к точке M за время δt оказывается равной величине:

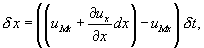
а скорость удаления или приближения к точке М вдоль координатной оси x определяется пределом отношения 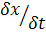при δt → 0, т.е.

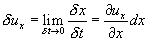
Т.о. любая точка частицы будет приближаться или удаляться от точки M вдоль оси x со скоростью, пропорциональной величине .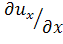

Очевидно, что, повторяя аналогичные рассуждения, найдем коэффициенты пропорциональности скоростей смещения по осям y и z в виде множителей.

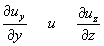
Кроме растяжения или сжатия, на скорости удаления выбранной точки от точки M по координате x скажутся деформация сдвига и поворот частицы в пространстве как твердого тела.

Очевидно, что эти добавки скорости пропорциональны быстроте изменения углов δθ и δγ.

Непосредственно из схемы деформации частицы вытекают такие соотношения:

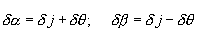
Выразим углы δγ и δθ

(*)

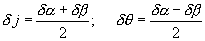Сами углы δα и δβ найдем, рассматривая вращение граней MN и ML относительно точки M.

Угловые смещения, как известно, равны линейным смещениям, деленным на радиус поворота.

Линейное смещение точки N относительно точки M вдоль оси x за время δt составит величину

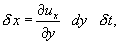
а угловое – соответственно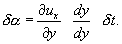

Так же находится угол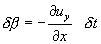

Знак минус здесь поставлен потому, что точка L движется относительно точки M в отрицательном направлении по оси y.

Подставляя найденные значения углов в формулы (*), деля интервал времени δt к нулю, получаем скорости скоса частицы в плоскости xy и вращения ее вокруг оси z, т.е.

Скос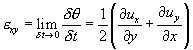

Вращение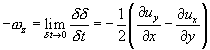

Знак минус перед 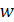_z означает вращение частицы вокруг оси z по часовой стрелке, т.к. мы уславливаемся считать положительным направлением вращения против часовой стрелки (от оси x к оси y).

Т.о. скорость смещения любой точки внутри элементарного кубика относительно точки M в направлении оси x оказывается пропорциональна величинам:

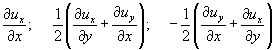
Мы рассмотрим только деформацию и вращение в плоскости xy.

Легко убедиться, что смещение по оси x вызывается аналогичными превращениями с частицей и в плоскости xz, а в плоскости zy коэффициенты пропорциональности равны нулю.

Поэтому полный набор коэффициентов такой:

(**)

(***)

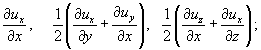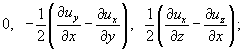Сравним найденные коэффициенты с первой строкой тензора ( ∙ )* в формуле (4.8) и сразу увидим, что они тождественно совпадают с его элементами. Причем группа (**) дает верхнюю строку симметричного тензора, а группа (***) – антисимметричную.

Очевидно, что если провести аналогичные рассуждения для отыскания коэффициентов, определяющих смещение точек жидкой частицы относительно ее полюса (точки M) по осям y и z, то получим весь набор элементов тензора ( ∙ )*.

При этом первая группа (**) опишет деформационное движение частицы, а вторая группа (***) - вращательное.

Т.о. неоднородность поля скоростей в любой точке пространства, занятого движущейся жидкостью, обусловлена деформационным и вращательным движением ее частичек, что выражается симметричной и кососимметричной частями тензора ( ∙ )*.

Симметричная часть тензора ( ∙ )* поэтому называется тензором скоростей деформации и обозначается def , а кососимметричная – вихрем скорости – vort

т.о. 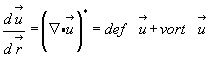(4.9)

и с учетом (4.7) получим

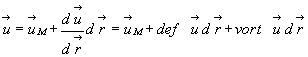(4.10)

Уравнение (4.10) представляет собой важное для гидродинамики утверждение, известное под названием теорема Коши-Гельмгольца:

Движение любой точки жидкой частицы можно рассматривать как результат сложения поступательного движения по траектории вместе с некоторой начальной точкой (точкой M в рассмотренном примере), вращательного движения вокруг оси, проходящей через начальную точку, и деформационного движения, которое, в свою очередь состоит из осевой деформации и деформации сдвига.

Замечание:

1. Теорема Коши-Гельмгольца раскрывает физическое содержание введенного нами тензора .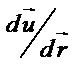

2. Тензор ( ∙ )* можно разложить множеством различных способов. При этом получатся какие-то другие варианты движения жидкой частицы. С математической точки зрения все они одинаково правомерны. Поэтому в теореме говорится «можно рассматривать», а не «следует рассматривать».

В курсе гидродинамики, однако, будем подразумевать категоричное утверждение «следует рассматривать».