I.5.4 НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЁТА. СИЛЫ ИНЕРЦИИ

Системы отсчёта, движущиеся относительно инерциальной системы с ускорением, называются неинерциальными. В неинерциальных системах отсчёта законы Ньютона не выполняются. Покой или движение материальных точек и тел в неинерциальных системах отсчёта описывают уравнениями, по форме аналогичными уравнению второго закона Ньютона, но в уравнения вводятся силы инерции.

Силы инерции обусловлены ускоренным движением системы отсчёта относительно измеряемой системы, поэтому в общем случае нужно учитывать следующие случаи проявления этих сил:

1) силы инерции 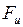при ускоренном поступательном движении системы отсчёта. Например, силы инерции проявляются при торможении поезда (она будет направлена в противоположную сторону движения и пассажир отклоняется от спинки сиденья), либо при наборе поездом скорости (пассажир, сидящий по ходу поезда, прижимается к спинке сиденья) и т.д.

2) Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчёта. В этом случае речь идёт о центробежных силах инерции .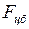

Центробежная сила – сила инерции; она противодействует изменению состояния движения и направлена от центра вращения. Иначе говоря, центробежная сила – сила инерции, противодействующая центростремительной силе (рис. 36).

Центробежные силы действуют на тела во вращающихся системах отсчёта в направлении радиуса от оси вращения (как это было отмечено выше) и зависят от угловой скорости вращения системы и радиуса, но не зависят от скорости тел относительно вращающихся систем отсчёта. Следовательно, центробежная сила инерции действует во вращающихся системах отсчёта на все тела, удалённые от оси вращения на конечное расстояние, независимо от того, покоятся они в этой системе или движутся относительно неё с какой-то скоростью.

Центробежная сила определяется по формуле:

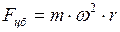, (I.138)

где 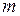- масса тела; 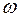- угловая скорость тела; 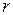- радиус окружности.

Действию центробежных сил инерции подвергаются, например, пассажиры в движущемся транспорте на поворотах.

3) Силы инерции, действующие на тело, движущееся во вращающейся системе отсчёта. Если во вращающейся системе отсчёта некое тело движется по радиусу от центра или к центру вращения, то его скорость изменяется. Тело приобретает тангенциальное ускорение, которое вызывается силой Кориолиса .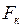

Сила Кориолиса определяется по формуле:

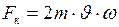, (I.139)

где 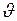- постоянная по величине скорость тела, направленная по радиусу;

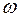- угловая скорость вращающейся системы отсчёта;

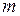- масса тела.

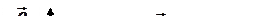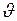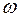Формула (I.139) справедлива и в том случае, когда и не постоянны. Тогда эта формула позволяет определить мгновенное значение силы Кориолиса.

Рисунок 37 – Направление силы Кориолиса, в соответствии с правилом правого винта.

Вектор 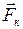перпендикулярен векторам скорости 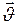тела и угловой скорости вращения 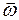системы отсчёта в соответствии с правилом правого винта (рис.37).

Распределение теплоты на земной поверхности обусловливает морские и воздушные течения (ветры). Под влиянием силы Кориолиса ветры испытывают в северном полушарии отклонение вправо, в южном полушарии – влево. Морское течение Гольфстрим отклоняется вправо от северного направления. Движение ветра при барометрических максимумах и минимумах (в антициклонах и циклонах) также отклоняется кориолисовыми силами.

Влияние сил Кориолиса на массы текущей в реках воды в северном полушарии приводит к перемещению рек вправо, пока они не достигнут возвышенностей (закон Бэра). Этим объясняется часто наблюдаемое явление: правый берег реки в северном полушарии выше, чем левый.

Основной закон динамики для неинерциальных систем отсчёта:

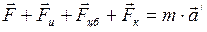, (I.140)

где 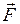- силы, обусловленные воздействием тел друг на друга, сообщающие телу ускорение ;

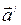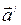- ускорение, которым обладают тела в неинерциальной системе отсчёта;

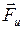- сила инерции;

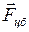- центробежная сила инерции;

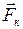- сила Кориолиса.

Необходимо обратить внимание на то, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчёта. Поэтому они не подчиняются третьему закону Ньютона, так как если на какое-либо тело действует сила инерции, то не существует противодействующей силы, приложенной к данному телу.

Для любого из тел, находящихся в неинерциальной системе отсчёта, силы инерции являются внешними; следовательно, здесь нет замкнутых систем.

Аналогия между силами инерции и силами тяготения положена в основу принципа эквивалентности гравитационных сил и сил инерции (принципа эквивалентности Эйнштейна), который является локальным принципом.

Принцип эквивалентности Эйнштейна: все физические явления в поле тяготения происходят совершенно так же, как и в соответствующем поле сил инерции, если напряжённости обоих полей в соответствующих точках пространства совпадают, а прочие начальные условия для рассматриваемых тел одинаковы. Этот принцип является основой общей теории относительности (см. в главе I.7).