Ускорения точек тела при плоскопараллельном движении. Векторная формула сложения ускорений.

Зависимости для ускорений двух точек плоской фигуры можно получить дифференцируя формулу сложения скоростей. С учетом (2.30) формула (2.29) примет вид

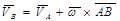
Дифференцируя по времени обе части этого равенства получим

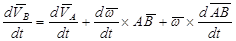(2.31)

здесь 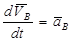, 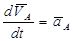- ускорения точек В и А относительно неподвижной системы координат (рис. 2.24, а);

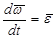- угловое ускорение плоской фигуры, .

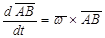Учитывая эти соотношения, выражение (2.31) можно записать в виде

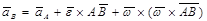или

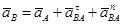(2.32)

где 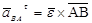, касательное ускорение перпендикулярно отрезку АВ и направлено по дуговой стрелке углового ускорения 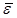тела, по модулю 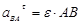, ,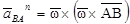нормальное ускорение направлено от точки В к полюсу А, по модулю .

	а)		б)

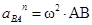Рисунок 2.24. К определению ускорения точки

при плоскопараллельном движении твердого тела

Выражение (2.32) называется векторной формулой сложения ускорений.

Теорема о сложении ускорений: ускорение любой точки твердого тела при его плоскопараллельном движении складывается из ускорения в поступательном движении точки вместе с полюсом и ускорения точки во вращательном движении вокруг полюса.