Плоскопараллельное движение твердого тела

Плоскопараллельным называется такое движение твердого тела, при котором все его точки движутся параллельно некоторой неподвижной плоскости. Пусть твердое тело совершает плоское движение относительно неподвижной плоскости П₀ (рис. 2.12). Тогда любая прямая, перпендикулярная этой плоскости и жестко скрепленная с телом, будет двигаться поступательно, а все точки этой прямой двигаться одинаково.

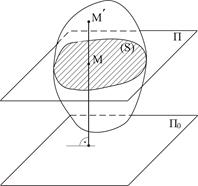
Рисунок 2.12

Для изучения движения точек, лежащих на рассматриваемой прямой, достаточно изучить движение одной точки этой прямой.

Рассуждая аналогично относительно любой прямой, перпендикулярной П₀ и скрепленной с телом, можно сделать вывод, что для изучения плоскопараллельного движения твердого тела достаточно изучить движение точек этого тела, лежащих в какой-либо плоскости П, параллельной неподвижной плоскости П₀ и образующих плоскую фигуру S.

Положение плоской фигуры S в плоскости Оxy определяется положением отрезка прямой АВ (рис. 2.13). В свою очередь положение отрезка АВ можно определить, зная координаты x_A , y_A точки А и угол , который образует отрезок АВ с осью x.

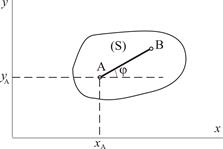
Рисунок 2.13

Точку А, выбранную для определения положения фигуры S, называют полюсом. При движении величины x_A , y_A и φ будут изменяться. Чтобы знать закон движения надо знать зависимости

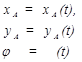(2.28)

Выражения (2.28) являются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твердого тела.

Плоскопараллельное движение твердого тела можно представить в виде совокупности поступательного движения вместе с полюсом и вращательного движения в плоскости тела вокруг оси, проходящей через выбранный полюс (рис.2.14).

Возьмем точку А и свяжем с ней подвижную систему координат Ax₁y₁z₁, оси которой будут двигаться поступательно с точкой А тела (рис. 2.15).

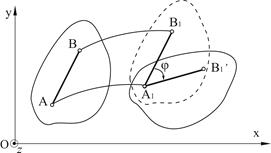
Рисунок 2.14

Тогда относительно подвижной системы координат тело совершает вращательное движение вокруг оси Az₁, перпендикулярной плоскости рисунка.

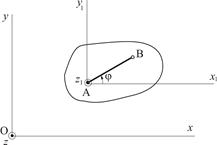
Рисунок 2.15