Скорости и ускорения точек тела при вращательном движении

Известно уравнение вращения твердого тела вокруг неподвижной оси 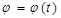.Расстояние s до точки М, отсчитываемое по дуге окружности от точки М₀, выражается зависимостью

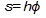(2.24)

где h – радиус окружности, по которой перемещается точка при вращении тела (рис.2.10).

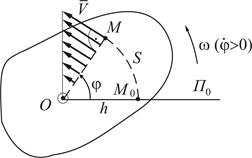
Рисунок 2.10

Алгебраическую скорость точки М определяем по формуле

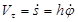
Модуль скорости точки М

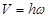(2.25)

Скорости точек тела, расположенных на отрезке прямой ОМ распределены по линейному закону. Скорости точек направлены по касательным к траекториям и перпендикулярны радиусам вращения.

Ускорение точки раскладывается на касательную и нормальную составляющие

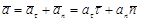(2.26)

Касательное и нормальное ускорения вычисляются по формулам

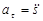
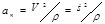
Учитывая (2.24) получим 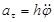, , 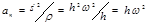так как

радиус окружности кривизны 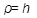. Таким образом

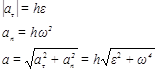(2.27)

Касательное, нормальное и полные ускорения точки, как и скорости, распределены по линейному закону. Они линейно зависят от расстояний точек до оси вращения. Нормальное ускорение направлено по радиусу окружности к оси вращения. Направление касательного ускорения зависит от знака алгебраического углового ускорения и направлено в сторону дуговой стрелки ε (рис. 2.11).

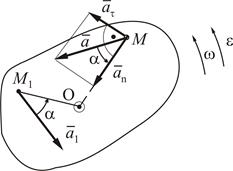
Рисунок 2.11

Обозначим α угол между полным ускорением точки и ее радиусом вращения, получим 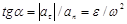. Угол α для всех точек тела одинаков. Откладывать его следует от ускорения к радиусу вращения в направлении дуговой стрелки углового ускорения независимо от направления вращения твердого тела.