Площадь поверхности тела вращения
Рассмотрим тело, получаемое вращением криволинейной трапеции.
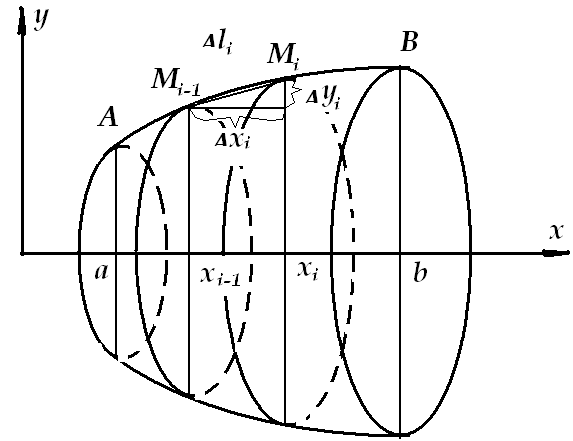 Будем предполагать, что функция
Будем предполагать, что функция 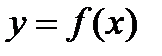 непрерывная и имеет непрерывную производную во всех точках отрезка
непрерывная и имеет непрерывную производную во всех точках отрезка 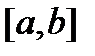 . Разобьём кривую
. Разобьём кривую 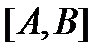 на части точками
на части точками 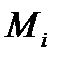 и проведем хорды
и проведем хорды 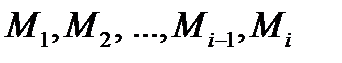 . Длины хорд обозначим через
. Длины хорд обозначим через 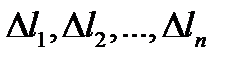 . Каждая хорда длины
. Каждая хорда длины 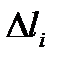 при вращение опишет усеченный конус, площадь поверхности которого:
при вращение опишет усеченный конус, площадь поверхности которого:
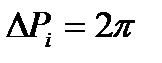
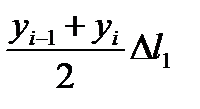 , где
, где
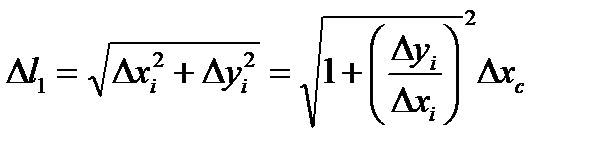
Функция 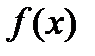 удовлетворяет всем условиям теоремы Лагранжа, следовательно, на отрезке
удовлетворяет всем условиям теоремы Лагранжа, следовательно, на отрезке 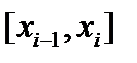 существует точка
существует точка 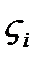 такая, что
такая, что 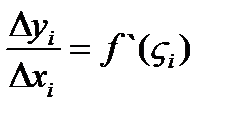 , следовательно, площадь поверхности усеченного конуса может быть представлена в виде:
, следовательно, площадь поверхности усеченного конуса может быть представлена в виде: 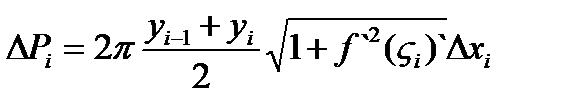 .
.
Площадь поверхности, образованная всеми усеченными конусами, определяется:
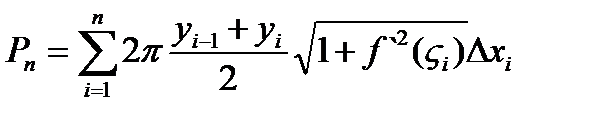
Принято считать, что площадь поверхности тела вращения определяется пределом:
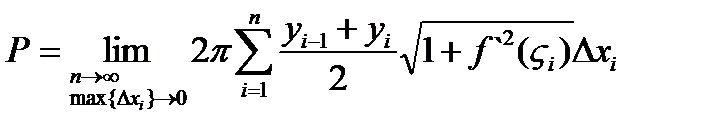 (3)
(3)
Таким образом, необходимо вычислить предел (3).
Представим величины 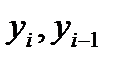 в виде
в виде 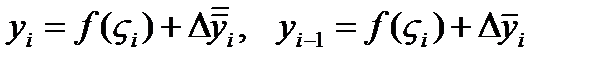 .
.
Подставляя в (3) получим:
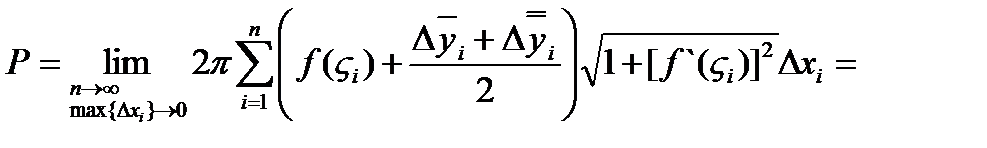
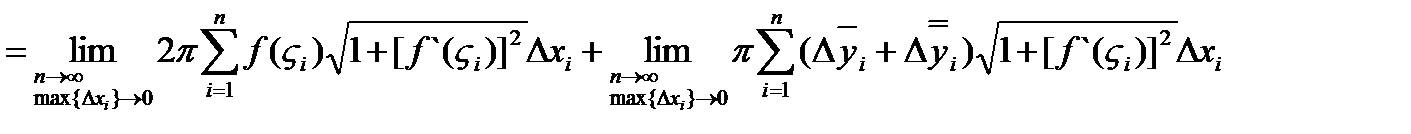
Величина первого предела определяется определенным интегралом:
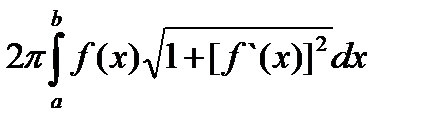
Сумма двух бесконечно малых величин представляет собой бесконечно малую величину, поэтому второй предел можно представить в виде:
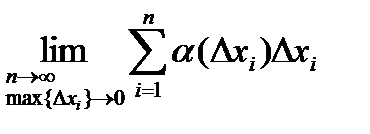 , где
, где 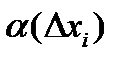 - бесконечно малая величина.
- бесконечно малая величина.
Оценим выражение, стоящее под знаком второго предела. По определению бесконечно малой величины для положительной величины 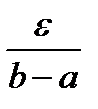 найдется такое положительное число
найдется такое положительное число 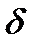 , что для всех величин
, что для всех величин 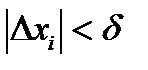 будет выполняться неравенство:
будет выполняться неравенство: 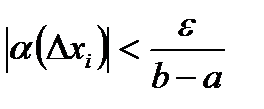 .
.
Следовательно, 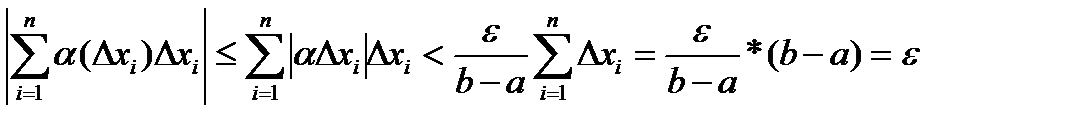
Таким образом, показали, что второй предел равен нулю при 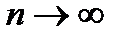 , и при стремлении диаметра разбиения к 0.
, и при стремлении диаметра разбиения к 0.
Следовательно, площадь поверхности тела вращения при сделанных ограничениях на функцию 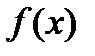 определяется выражением:
определяется выражением:
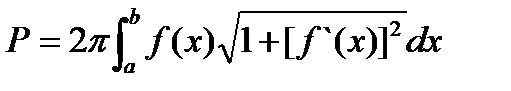 .
.
Пример: Определить площадь поверхности параболоида, образованного путём вращения параболы 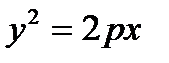 вокруг оси ох, при изменении х на отрезке
вокруг оси ох, при изменении х на отрезке 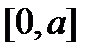 .
.
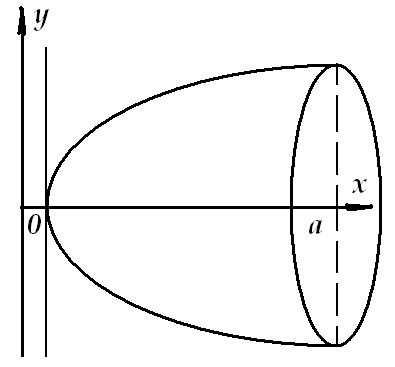
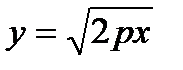 ,
, 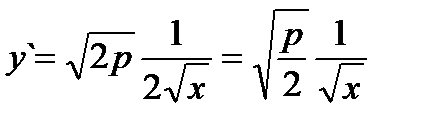
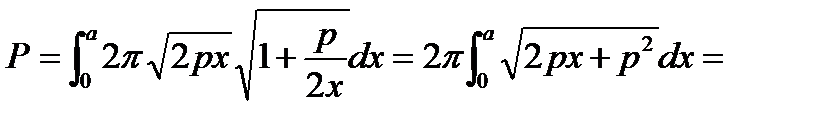
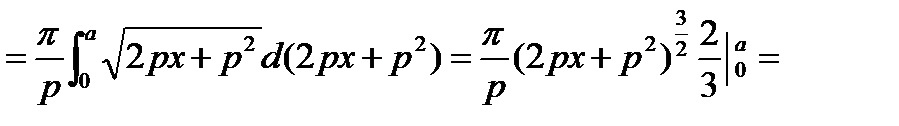
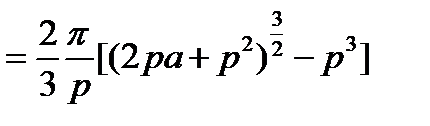 .
.
Дата добавления: 2017-06-13; просмотров: 1696;











