Вычисление объема тела по площадям параллельных сечений.
Рассмотрим некоторое тело Т…
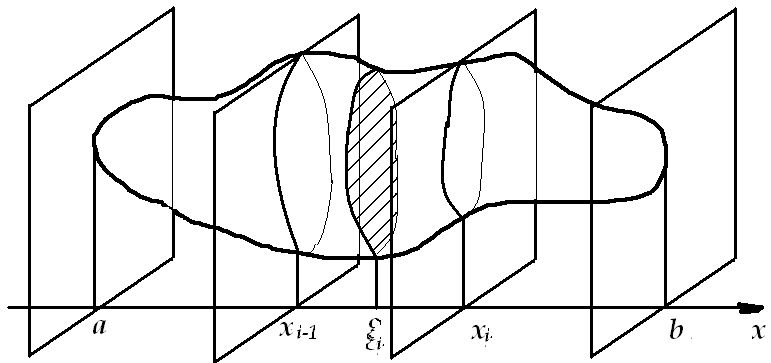
Предположим, что известна площадь любого сечения тела плоскостью, перпендикулярной оси ox. Эта площадь будет зависеть от положения секущей плоскости, т.е. будет являться функцией от переменной х. Будем считать, что 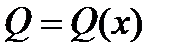 , есть непрерывная функция на отрезке
, есть непрерывная функция на отрезке 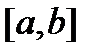 . Проведем плоскости
. Проведем плоскости 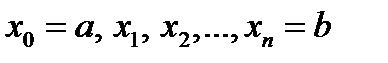 . Эти плоскости разбивают тело на слои, в каждом частичном отрезке выберем точку
. Эти плоскости разбивают тело на слои, в каждом частичном отрезке выберем точку 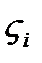 . Проведем через точку плоскость перпендикулярную оси ox. Соответствующая площадь
. Проведем через точку плоскость перпендикулярную оси ox. Соответствующая площадь 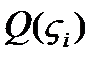 . На основании выделенного сечения построим цилиндр с образующей параллельной оси ох, объем цилиндра равен
. На основании выделенного сечения построим цилиндр с образующей параллельной оси ох, объем цилиндра равен 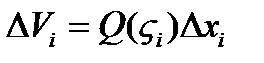 . Объем всех построенных таким образом цилиндров
. Объем всех построенных таким образом цилиндров 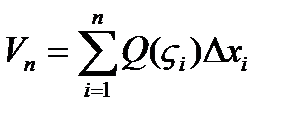 .
.
Объемом тела Т принято считать предел суммы 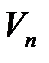 при
при 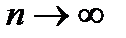 и при стремление диаметра разбиения к 0.
и при стремление диаметра разбиения к 0.
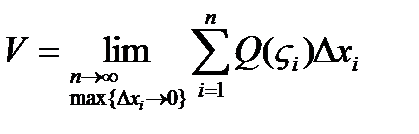 ,
,
Таким образом, при известных площадях сечений, вычисление объема тела сводится к вычислению определенного интеграла. 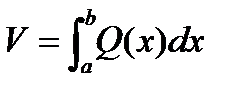
Пример: Вычислить объем трёхосного эллипсоида.
Уравнение эллипсоида имеет вид 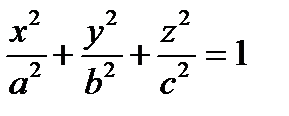
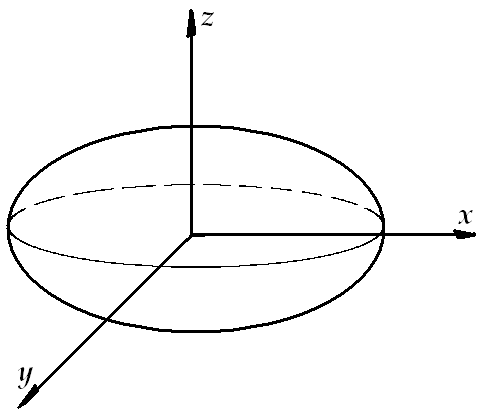 В сечение эллипсоида плоскостью перпендикулярной оси ох будут эллипсы, уравнение которых имеет вид:
В сечение эллипсоида плоскостью перпендикулярной оси ох будут эллипсы, уравнение которых имеет вид:
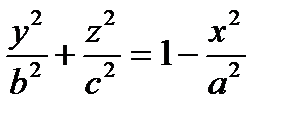 ,
, 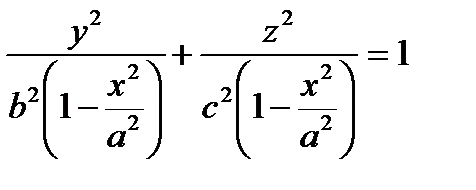 .
.
Полуоси эллипса 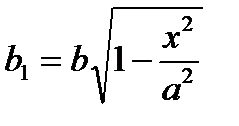 ,
, 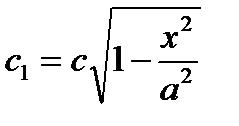 .
.
Ранее было показано, что площадь эллипса имеет вид: 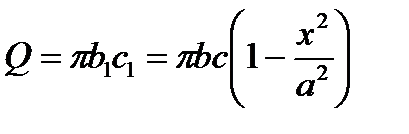 .
.
Объем эллипсоида будет определятся интегралом:
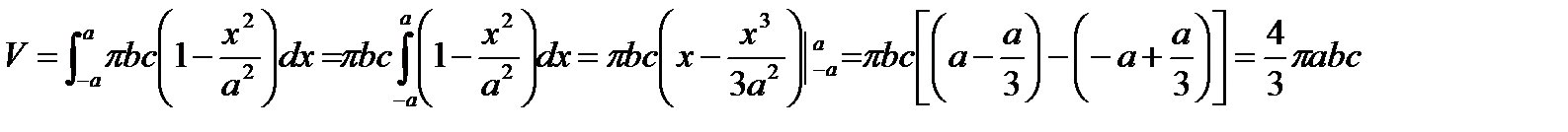 .
.
Частным случаем эллипсоида является шар => 
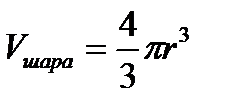
Дата добавления: 2017-06-13; просмотров: 3209;











